# MathParser.org-mXparser
**Repository Path**: afunc233/MathParser.org-mXparser
## Basic Information
- **Project Name**: MathParser.org-mXparser
- **Description**: Math Parser Java Android C# .NET/MONO (.NET Framework, .NET Core, .NET Standard, .NET PCL, Xamarin.Android, Xamarin.iOS) CLS Library - a super easy, rich and flexible mathematical expression parser (expression evaluator, expression provided as plain text / strings) for JAVA and C#. Main features: rich built-in library of operators, constants, math functions, user defined: arguments, functions, recursive functions and general recursion (direct / indirect). Additionally parser provides grammar and internal syntax checking.
- **Primary Language**: Unknown
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 1
- **Forks**: 0
- **Created**: 2020-11-10
- **Last Updated**: 2025-03-05
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# Package installation
## Nuget
PM> Install-Package MathParser.org-mXparser -Version 4.4.2
## Maven
org.mariuszgromada.math
MathParser.org-mXparser
4.4.2
# Scalar Scientific Calculator, Charts & Scripts - my new project
[](https://play.google.com/store/apps/details?id=org.mathparser.scalar.lite)
### Scalar in action
[](https://youtu.be/HUlEUaioogQ)
### Scalar - Free version
[ ](https://play.google.com/store/apps/details?id=org.mathparser.scalar.lite&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
### Scalar Pro - Full paid version
[
](https://play.google.com/store/apps/details?id=org.mathparser.scalar.lite&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
### Scalar Pro - Full paid version
[ ](https://play.google.com/store/apps/details?id=org.mathparser.scalar.pro&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
# MathParser.org-mXparser


# mXparser - optional donation
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser - a super easy, rich and highly flexible Mathematical Expression Parser (Math Parser, Expression Evaluator) library for JAVA, Android and C# .NET.
### 15.10.2020: first 500000 downloads!
### 20.12.2019: first 250000 downloads!
### 01.01.2019: first 100000 downloads!
### 01.08.2018: first 60000 downloads!
### 20.11.2017: first 20000 downloads!
### 01.09.2017: first 15000 downloads!
### 04.05.2017: first 10000 downloads!
### 31.03.2016: first 1000 downloads!

**mXparser** is **a highly flexible parser of mathematical expressions provided as text**. Software delivers easy to use API for JAVA and C# .NET.
# Supported frameworks

- JAVA: 6+
- Android - tested with mxparser compiled using jdk 1.7
- .NET Framework (2+) / MONO CLS
- .NET Core: 1+
- .NET Standard: 1+
- .NET PCL
- Xamarin

# JAVA intro
# C# intro
# Tutorial

# [>>> Click to learn from examples <<<](http://mathparser.org/mxparser-tutorial/)
# Main functionalities:
- **basic operators**, i.e.: +, -, *, ^, !
- **[Boolean logic](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BooleanAlgebra.html)** operators i.e.: or, and, xor
- **[binary relations](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BinaryRelations.html)** i.e.: =, <, >
- **[math functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html)** (large library of 1-arg, 2-arg, 3-arg - functions) i.e.: sin, cos, Stirling numbers, log, inverse functions
- **[constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathConstants.html)** (large library), i.e.: pi, e, golden ratio
- **n-args functions**, i.e.: [greatest common divisor](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html#gcd-int...-)
- **[iterated summation and product operators](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumberTheory.html#sigmaSummation-org.mariuszgromada.math.mxparser.Expression-org.mariuszgromada.math.mxparser.Argument-double-double-double-)**
- **[differentiation and integration](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumericalAnalysis.html)**
# High flexibility functionalities
- **[user defined constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Constant.html)** and arguments, both free - and dependent on other arguments + possibility of use in functions
- **[user defined functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html)** (both free and depended)
- **[user defined recursive arguments](http://mathparser.org/api/org/mariuszgromada/math/mxparser/RecursiveArgument.html)** + simple (controlled) recursion (1 recursive argument)
- **[user defined recursive functions / expressions (any)](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html#getRecursiveMode--)** - complex, many arguments, no limitation
- **[internal syntax checking](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#checkSyntax--)**
- **[internal help](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getHelp--)**
- other useful functionalities, i.e.: [computing time](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getComputingTime--), expression description.
# Project documentation
### - [mXparser - API (english)](http://mathparser.org/api/)
### - [mXparser - WIKI (english)](https://github.com/mariuszgromada/MathParser.org-mXparser/wiki)
### - [mXparser - Tutorial (english)](http://mathparser.org/mxparser-tutorial/)
### - [MathSpace.pl - site about math with mXparser examples (polish)](http://mathspace.pl/)
### - [MathParser.org - site about mXparser (english)](http://mathparser.org/)
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser in nutshell
#### You want simple calculator...
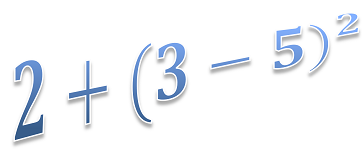
Expression e = new Expression("2+3");
e.calculate();
:+1:
#### A calculator supporting parenthesis...

Expression e = new Expression("2+(3-5)^2");
e.calculate();
:+1:
#### You care about predefined constants...

Expression e = new Expression("2*pi");
e.calculate();
:+1:
#### You need to define your own constants...
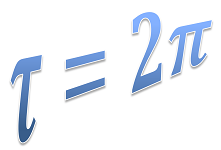
Constant tau = new Constant("tau = 2*pi");
Expression e = new Expression("3*tau", tau);
e.calculate();
:+1:
#### You enjoy using many built-in functions...

Expression e = new Expression("sin(2*pi)");
e.calculate();
:+1:
#### You do not limit yourself to unary functions...
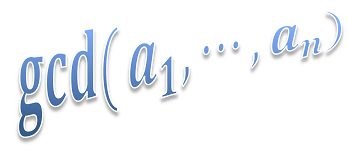
Expression e = new Expression("gcd(2,5,10,30)");
e.calculate();
:+1:
#### What about user defined arguments...
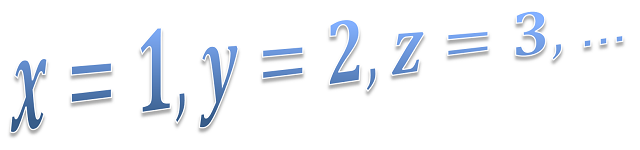
Argument x = new Argument("x = 5");
Expression e = new Expression("sin(x)");
e.calculate();
:+1:
#### You are considering dependent arguments...

Argument x = new Argument("x = 5");
Argument y = new Argument("y = 2*x", x);
Expression e = new Expression("sin(y)", y);
e.calculate();
:+1:
#### You need to apply some logic...

Argument x = new Argument("x = 5");
Expression e = new Expression("if(sin(x) > 5, 1, 0)", x);
e.calculate();
:+1:
#### Yes, you are right, there is a support for Boolean algebra!

Expression e = new Expression("5=6");
e.calculate();
:+1:
#### And for binary relations as well!
Expression e = new Expression("5 <= 6");
e.calculate();
:+1:
## mXparser is cool! But this is only the begging, we are just warming up!
#### You want to play with iterated operators...

Expression e = new Expression("sum(i, 1, 10, 2*i^2 + pi)");
e.calculate();
:+1:
#### You want to iterate differently by not necessarily whole numbes...

Expression e = new Expression("prod(i, 1, 5, i, 0.5)");
e.calculate();
:+1:
#### You want to have more fun with math...
Argument x = new Argument("x = pi/2");
Expression e20 = new Expression("sum(n,0,10,(-1)^n*(x^(2*n+1))/(2*n+1)!)", x);
e.calculate();
:+1:
#### You still want more fun with calculus operations, i.e. differentiation...
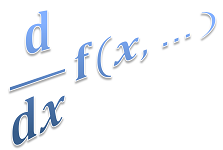
Argument x = new Argument("x = pi/2");
Expression e = new Expression("cos(x)-der(sin(x), x)", x);
e.calculate();
:+1:
#### And definite integrals as well...
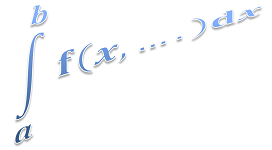
Expression e = new Expression("2*int(sqrt(1-x^2), x, -1, 1)");
e.calculate();
:+1:
## mXparser is even cooler! It is time to ask about ...
#### user defined functions...
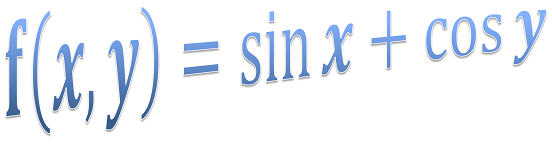
Function f = new Function("f(x,y) = sin(x) + cos(y)");
f.calculate(1,2);
Expression e = new Expression("f(1,2) - 10", f);
e.calculate();
:+1:
#### Recursion is your desire...
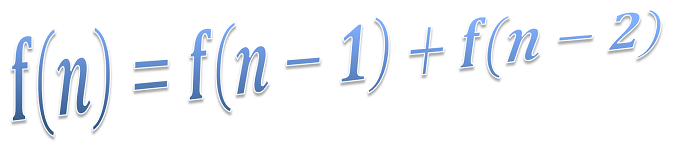
Function f = new Function("f(n) = if( n>0, n*f(n-1), 1)");
f.calculate()
:+1:
#### Any kind of recursion...
Function Cnk = new Function("Cnk(n,k) = if(k>0, if(k |Boolean Operator|Implication (IMP)|p --> q|1.0|
| <-- |Boolean Operator|Converse implication (CIMP)|p <-- q|1.0|
| -/> |Boolean Operator|Material nonimplication (NIMP)|p -/> q|1.0|
| |Boolean Operator|Logical biconditional (EQV)|p <-> q|1.0|
| ~ |Boolean Operator|Negation|~p|1.0|
## Bitwise Operators
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| @~ |Bitwise Operator|Bitwise unary complement|@~10|4.0|
| @& |Bitwise Operator|Bitwise AND|10 @& 2|4.0|
| @^ |Bitwise Operator|Bitwise exclusive OR|10 @^ 2|4.0|
| @\| |Bitwise Operator|Bitwise inclusive OR|10 @\| 2|4.0|
| @<< |Bitwise Operator|Signed left shift|10 @<< 2|4.0|
| @>> |Bitwise Operator|Signed right shift|10 @>> 2|4.0|
## Binary Relations
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| = |Binary Relation|Equality|a = b|1.0|
| == |Binary Relation|Equality|a == b|1.0|
| <> |Binary Relation|Inequation|a <> b|1.0|
| ~= |Binary Relation|Inequation|a ~= b|1.0|
| != |Binary Relation|Inequation|a != b|1.0|
| < |Binary Relation|Lower than|a < b|1.0|
| > |Binary Relation|Greater than|a > b|1.0|
| <= |Binary Relation|Lower or equal|a <= b|1.0|
| >= |Binary Relation|Greater or equal|a >= b|1.0|
## Unary Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| sin | Unary Function | Trigonometric sine function | sin(x) | 1.0 |
| cos | Unary Function | Trigonometric cosine function | cos(x) | 1.0 |
| tg | Unary Function | Trigonometric tangent function | tg(x) | 1.0 |
| tan | Unary Function | Trigonometric tangent function | tan(x) | 1.0 |
| ctg | Unary Function | Trigonometric cotangent function | ctg(x) | 1.0 |
| cot | Unary Function | Trigonometric cotangent function | cot(x) | 1.0 |
| ctan | Unary Function | Trigonometric cotangent function | ctan(x) | 1.0 |
| sec | Unary Function | Trigonometric secant function | sec(x) | 1.0 |
| csc | Unary Function | Trigonometric cosecant function | csc(x) | 1.0 |
| cosec | Unary Function | Trigonometric cosecant function | cosec(x) | 1.0 |
| asin | Unary Function | Inverse trigonometric sine function | asin(x) | 1.0 |
| arsin | Unary Function | Inverse trigonometric sine function | arsin(x) | 1.0 |
| arcsin | Unary Function | Inverse trigonometric sine function | arcsin(x) | 1.0 |
| acos | Unary Function | Inverse trigonometric cosine function | acos(x) | 1.0 |
| arcos | Unary Function | Inverse trigonometric cosine function | arcos(x) | 1.0 |
| arccos | Unary Function | Inverse trigonometric cosine function | arccos(x) | 1.0 |
| atg | Unary Function | Inverse trigonometric tangent function | atg(x) | 1.0 |
| atan | Unary Function | Inverse trigonometric tangent function | atan(x) | 1.0 |
| arctg | Unary Function | Inverse trigonometric tangent function | arctg(x) | 1.0 |
| arctan | Unary Function | Inverse trigonometric tangent function | arctan(x) | 1.0 |
| actg | Unary Function | Inverse trigonometric cotangent function | actg(x) | 1.0 |
| acot | Unary Function | Inverse trigonometric cotangent function | acot(x) | 1.0 |
| actan | Unary Function | Inverse trigonometric cotangent function | actan(x) | 1.0 |
| arcctg | Unary Function | Inverse trigonometric cotangent function | arcctg(x) | 1.0 |
| arccot | Unary Function | Inverse trigonometric cotangent function | arccot(x) | 1.0 |
| arcctan | Unary Function | Inverse trigonometric cotangent function | arcctan(x) | 1.0 |
| ln | Unary Function | Natural logarithm function (base e) | ln(x) | 1.0 |
| log2 | Unary Function | Binary logarithm function (base 2) | log2(x) | 1.0 |
| log10 | Unary Function | Common logarithm function (base 10) | log10(x) | 1.0 |
| rad | Unary Function | Degrees to radians function | rad(x) | 1.0 |
| exp | Unary Function | Exponential function | exp(x) | 1.0 |
| sqrt | Unary Function | Squre root function | sqrt(x) | 1.0 |
| sinh | Unary Function | Hyperbolic sine function | sinh(x) | 1.0 |
| cosh | Unary Function | Hyperbolic cosine function | cosh(x) | 1.0 |
| tgh | Unary Function | Hyperbolic tangent function | tgh(x) | 1.0 |
| tanh | Unary Function | Hyperbolic tangent function | tanh(x) | 1.0 |
| coth | Unary Function | Hyperbolic cotangent function | coth(x) | 1.0 |
| ctgh | Unary Function | Hyperbolic cotangent function | ctgh(x) | 1.0 |
| ctanh | Unary Function | Hyperbolic cotangent function | ctanh(x) | 1.0 |
| sech | Unary Function | Hyperbolic secant function | sech(x) | 1.0 |
| csch | Unary Function | Hyperbolic cosecant function | csch(x) | 1.0 |
| cosech | Unary Function | Hyperbolic cosecant function | cosech(x) | 1.0 |
| deg | Unary Function | Radians to degrees function | deg(x) | 1.0 |
| abs | Unary Function | Absolut value function | abs(x) | 1.0 |
| sgn | Unary Function | Signum function | sgn(x) | 1.0 |
| floor | Unary Function | Floor function | floor(x) | 1.0 |
| ceil | Unary Function | Ceiling function | ceil(x) | 1.0 |
| not | Unary Function | Negation function | not(x) | 1.0 |
| asinh | Unary Function | Inverse hyperbolic sine function | asinh(x) | 1.0 |
| arsinh | Unary Function | Inverse hyperbolic sine function | arsinh(x) | 1.0 |
| arcsinh | Unary Function | Inverse hyperbolic sine function | arcsinh(x) | 1.0 |
| acosh | Unary Function | Inverse hyperbolic cosine function | acosh(x) | 1.0 |
| arcosh | Unary Function | Inverse hyperbolic cosine function | arcosh(x) | 1.0 |
| arccosh | Unary Function | Inverse hyperbolic cosine function | arccosh(x) | 1.0 |
| atgh | Unary Function | Inverse hyperbolic tangent function | atgh(x) | 1.0 |
| atanh | Unary Function | Inverse hyperbolic tangent function | atanh(x) | 1.0 |
| arctgh | Unary Function | Inverse hyperbolic tangent function | arctgh(x) | 1.0 |
| arctanh | Unary Function | Inverse hyperbolic tangent function | arctanh(x) | 1.0 |
| acoth | Unary Function | Inverse hyperbolic cotangent function | acoth(x) | 1.0 |
| actgh | Unary Function | Inverse hyperbolic cotangent function | actgh(x) | 1.0 |
| actanh | Unary Function | Inverse hyperbolic cotangent function | actanh(x) | 1.0 |
| arcoth | Unary Function | Inverse hyperbolic cotangent function | arcoth(x) | 1.0 |
| arccoth | Unary Function | Inverse hyperbolic cotangent function | arccoth(x) | 1.0 |
| arcctgh | Unary Function | Inverse hyperbolic cotangent function | arcctgh(x) | 1.0 |
| arcctanh | Unary Function | Inverse hyperbolic cotangent function | arcctanh(x) | 1.0 |
| asech | Unary Function | Inverse hyperbolic secant function | asech(x) | 1.0 |
| arsech | Unary Function | Inverse hyperbolic secant function | arsech(x) | 1.0 |
| arcsech | Unary Function | Inverse hyperbolic secant function | arcsech(x) | 1.0 |
| acsch | Unary Function | Inverse hyperbolic cosecant function | acsch(x) | 1.0 |
| arcsch | Unary Function | Inverse hyperbolic cosecant function | arcsch(x) | 1.0 |
| arccsch | Unary Function | Inverse hyperbolic cosecant function | arccsch(x) | 1.0 |
| acosech | Unary Function | Inverse hyperbolic cosecant function | acosech(x) | 1.0 |
| arcosech | Unary Function | Inverse hyperbolic cosecant function | arcosech(x) | 1.0 |
| Sa | Unary Function | Sinc function (normalized) | Sa(x) | 1.0 |
| sinc | Unary Function | Sinc function (normalized) | sinc(x) | 1.0 |
| Sinc | Unary Function | Sinc function (unnormalized) | Sinc(x) | 1.0 |
| Bell | Unary Function | Bell number | Bell(n) | 1.0 |
| Luc | Unary Function | Lucas number | Luc(n) | 1.0 |
| Fib | Unary Function | Fibonacci number | Fib(n) | 1.0 |
| harm | Unary Function | Harmonic number | harm(n) | 1.0 |
| ispr | Unary Function | Prime number test (is number a prime?) | ispr(n) | 2.3 |
| Pi | Unary Function | Prime-counting function - Pi(x) | Pi(n) | 2.3 |
| Ei | Unary Function | Exponential integral function (non-elementary special function) - usage example: Ei(x) | Ei(x) | 2.3 |
| li | Unary Function | Logarithmic integral function (non-elementary special function) - usage example: li(x) | li(x) | 2.3 |
| Li | Unary Function | Offset logarithmic integral function (non-elementary special function) - usage example: Li(x) | Li(x) | 2.3 |
| erf | Unary Function | Gauss error function (non-elementary special function) - usage example: 2 + erf(x) | erf(x) | 3.0 |
| erfc | Unary Function | Gauss complementary error function (non-elementary special function) - usage example: 1 - erfc(x) | erfc(x) | 3.0 |
| erfInv | Unary Function | Inverse Gauss error function (non-elementary special function) - usage example: erfInv(x) | erfInv(x) | 3.0 |
| erfcInv | Unary Function | Inverse Gauss complementary error function (non-elementary special function) - usage example: erfcInv(x) | erfcInv(x) | 3.0 |
| ulp | Unary Function | Unit in The Last Place - ulp(0.1) | ulp(x) | 3.0 |
| isNaN | Unary Function | Returns true = 1 if value is a Not-a-Number (NaN), false = 0 otherwise - usage example: isNaN(x) | isNaN(x) | 4.1 |
| ndig10 | Unary Function | Number of digits in numeral system with base 10 | ndig10(x) | 4.1 |
| nfact | Unary Function | Prime decomposition - number of distinct prime factors | nfact(x) | 4.1 |
| arcsec | Unary Function | Inverse trigonometric secant | arcsec(x) | 4.1 |
| Gamma | Unary Function | Gamma special function Γ(s) | Gamma(x) | 4.3 |
| LambW0(x) | Unary Function | Lambert-W special function, principal branch 0, also called the omega function or product logarithm | LambW0(x) | 4.3 |
| LambW1(x) | Unary Function | Lambert-W special function, branch -1, also called the omega function or product logarithm | LambW1(x) | 4.3 |
| sgnGamma | Unary Function | Signum of Gamma special function, Γ(x) | sgnGamma(x) | 4.3 |
| logGamma | Unary Function | Log Gamma special function, lnΓ(x) | logGamma(x) | 4.3 |
| diGamma | Unary Function | Digamma function as the logarithmic derivative of the Gamma special function, ψ(x) | diGamma(x) | 4.3 |
## Binary Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| log | Binary Function | Logarithm function | log(a, b) | 1.0 |
| mod | Binary Function | Modulo function | mod(a, b) | 1.0 |
| C | Binary Function | Binomial coefficient function | C(n, k) | 1.0 |
| Bern | Binary Function | Bernoulli numbers | Bern(m, n) | 1.0 |
| Stirl1 | Binary Function | Stirling numbers of the first kind | Stirl1(n, k) | 1.0 |
| Stirl2 | Binary Function | Stirling numbers of the second kind | Stirl2(n, k) | 1.0 |
| Worp | Binary Function | Worpitzky number | Worp(n, k) | 1.0 |
| Euler | Binary Function | Euler number | Euler(n, k) | 1.0 |
| KDelta | Binary Function | Kronecker delta | KDelta(i, j) | 1.0 |
| EulerPol | Binary Function | EulerPol | EulerPol | 1.0 |
| Harm | Binary Function | Harmonic number | Harm(x, n) | 1.0 |
| rUni | Binary Function | Random variable - Uniform continuous distribution U(a,b), usage example: 2*rUni(2,10) | rUni(a, b) | 3.0 |
| rUnid | Binary Function | Random variable - Uniform discrete distribution U{a,b}, usage example: 2*rUnid(2,100) | rUnid(a, b) | 3.0 |
| round | Binary Function | Half-up rounding, usage examples: round(2.2, 0) = 2, round(2.6, 0) = 3, round(2.66,1) = 2.7 | round(x, n) | 3.0 |
| rNor | Binary Function | Random variable - Normal distribution N(m,s) m - mean, s - stddev, usage example: 3*rNor(0,1) | rNor(mean, stdv) | 3.0 |
| ndig | Binary Function | Number of digits representing the number in numeral system with given base | ndig(number, base) | 4.1 |
| dig10 | Binary Function | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - base 10 numeral system | dig10(num, pos) | 4.1 |
| factval | Binary Function | Prime decomposition - factor value at position between 1 ... nfact(n) - ascending order by factor value | factval(number, factorid) | 4.1 |
| factexp | Binary Function | Prime decomposition - factor exponent / multiplicity at position between 1 ... nfact(n) - ascending order by factor value | factexp(number, factorid) | 4.1 |
| root | Binary Function | N-th order root of a number | root(rootorder, number) | 4.1 |
| GammaL | Binary Function | Lower incomplete gamma special function, γ(s,x) | GammaL(s,x) | 4.3 |
| GammaU | Binary Function | Upper incomplete Gamma special function, Γ(s,x) | GammaU(s,x) | 4.3 |
| GammaP | Binary Function | Lower regularized P gamma special function, P(s,x) | GammaP(s,x) | 4.3 |
| GammaRegL | Binary Function | Lower regularized P gamma special function, P(s,x) | GammaRegL(s,x) | 4.3 |
| GammaQ | Binary Function | Upper regularized Q Gamma special function, Q(s,x) | GammaQ(s,x) | 4.3 |
| GammaRegU | Binary Function | Upper regularized Q Gamma special function, Q(s,x) | GammaRegU(s,x) | 4.3 |
| Beta | Binary Function | The Beta special function B(x,y), also called the Euler integral of the first kind | Beta(x,y) | 4.3 |
| logBeta | Binary Function | The Log Beta special function ln B(x,y), also called the Log Euler integral of the first kind, ln B(x,y) | logBeta(x,y) | 4.3 |
## 3-args Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| if | 3-args Function | If function | if( cond, expr-if-true, expr-if-false ) | 1.0 |
| chi | 3-args Function | Characteristic function for x in (a,b) | chi(x, a, b) | 1.0 |
| CHi | 3-args Function | Characteristic function for x in [a,b] | CHi(x, a, b) | 1.0 |
| Chi | 3-args Function | Characteristic function for x in [a,b) | Chi(x, a, b) | 1.0 |
| cHi | 3-args Function | Characteristic function for x in (a,b] | cHi(x, a, b) | 1.0 |
| pUni | 3-args Function | Probability distribution function - Uniform continuous distribution U(a,b) | pUni(x, a, b) | 3.0 |
| cUni | 3-args Function | Cumulative distribution function - Uniform continuous distribution U(a,b) | cUni(x, a, b) | 3.0 |
| qUni | 3-args Function | Quantile function (inverse cumulative distribution function) - Uniform continuous distribution U(a,b) | qUni(q, a, b) | 3.0 |
| pNor | 3-args Function | Probability distribution function - Normal distribution N(m,s) | pNor(x, mean, stdv) | 3.0 |
| cNor | 3-args Function | Cumulative distribution function - Normal distribution N(m,s) | cNor(x, mean, stdv) | 3.0 |
| qNor | 3-args Function | Quantile function (inverse cumulative distribution function) | qNor(q, mean, stdv) | 3.0 |
| dig | 3-args Function | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - numeral system with given base | dig(num, pos, base) | 4.1 |
| BetaInc | 3-args Function | The incomplete beta special function B(x; a, b), also called the incomplete Euler integral of the first kind | BetaInc(x,a,b) | 4.3 |
| BetaI | 3-args Function | The regularized incomplete beta (or regularized beta) special function I(x; a, b), also called the regularized incomplete Euler integral of the first kind | BetaI(x,a,b) | 4.3 |
| BetaReg | 3-args Function | The regularized incomplete beta (or regularized beta) special function I(x; a, b), also called the regularized incomplete Euler integral of the first kind | BetaReg(x,a,b) | 4.3 |
## Variadic Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| iff | Variadic Function | If function | iff( cond-1, expr-1; ... ; cond-n, expr-n ) | 1.0 |
| min | Variadic Function | Minimum function | min(a1, ..., an) | 1.0 |
| max | Variadic Function | Maximum function | max(a1, ..., an) | 1.0 |
| ConFrac | Variadic Function | Continued fraction | ConFrac(a1, ..., an) | 1.0 |
| ConPol | Variadic Function | Continued polynomial | ConPol(a1, ..., an) | 1.0 |
| gcd | Variadic Function | Greatest common divisor | gcd(a1, ..., an) | 1.0 |
| lcm | Variadic Function | Least common multiple | lcm(a1, ..., an) | 1.0 |
| add | Variadic Function | Summation operator | add(a1, ..., an) | 2.4 |
| multi | Variadic Function | Multiplication | multi(a1, ..., an) | 2.4 |
| mean | Variadic Function | Mean / average value | mean(a1, ..., an) | 2.4 |
| var | Variadic Function | Bias-corrected sample variance | var(a1, ..., an) | 2.4 |
| std | Variadic Function | Bias-corrected sample standard deviation | std(a1, ..., an) | 2.4 |
| rList | Variadic Function | Random number from given list of numbers | rList(a1, ..., an) | 3.0 |
| coalesce | Variadic Function | Returns the first non-NaN value | coalesce(a1, ..., an) | 4.1 |
| or | Variadic Function | Logical disjunction (OR) - variadic | or(a1, ..., an) | 4.1 |
| and | Variadic Function | Logical conjunction (AND) - variadic | and(a1, ..., an) | 4.1 |
| xor | Variadic Function | Exclusive or (XOR) - variadic | xor(a1, ..., an) | 4.1 |
| argmin | Variadic Function | Arguments / indices of the minima | argmin(a1, ..., an) | 4.1 |
| argmax | Variadic Function | Arguments / indices of the maxima | argmax(a1, ..., an) | 4.1 |
| med | Variadic Function | The sample median | med(a1, ..., an) | 4.1 |
| mode | Variadic Function | Mode - the value that appears most often | mode(a1, ..., an) | 4.1 |
| base | Variadic Function | Returns number in given numeral system base represented by list of digits | base(b, d1, ..., dn) | 4.1 |
| ndist | Variadic Function | Number of distinct values | ndist(v1, ..., vn) | 4.1 |
## Calculus Operators / Iterated Operators
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| sum | Calculus Operator | Summation operator - SIGMA | sum( i, from, to, expr , ) | 1.0 |
| prod | Calculus Operator | Product operator - PI | prod( i, from, to, expr , ) | 1.0 |
| int | Calculus Operator | Definite integral operator | int( expr, arg, from, to ) | 1.0 |
| der | Calculus Operator | Derivative operator | der( expr, arg, ) | 1.0 |
| der- | Calculus Operator | Left derivative operator | der-( expr, arg, ) | 1.0 |
| der+ | Calculus Operator | Right derivative operator | der+( expr, arg, ) | 1.0 |
| dern | Calculus Operator | n-th derivative operator | dern( expr, n, arg ) | 1.0 |
| diff | Calculus Operator | Forward difference operator | diff( expr, arg, ) | 1.0 |
| difb | Calculus Operator | Backward difference operator | difb( expr, arg, ) | 1.0 |
| avg | Calculus Operator | Average operator | avg( i, from, to, expr , ) | 2.4 |
| vari | Calculus Operator | Bias-corrected sample variance operator | vari( i, from, to, expr , ) | 2.4 |
| stdi | Calculus Operator | Bias-corrected sample standard deviation operator | stdi( i, from, to, expr , ) | 2.4 |
| mini | Calculus Operator | Minimum value | mini( i, from, to, expr , ) | 2.4 |
| maxi | Calculus Operator | Maximum value | maxi( i, from, to, expr , ) | 2.4 |
| solve | Calculus Operator | f(x) = 0 equation solving, function root finding | solve( expr, a, b ) | 4.0 |
## Random Variables
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [Uni] |Random Variable|Random variable - Uniform continuous distribution U(0,1), usage example: 2*[Uni]|2*[Uni]|3.0|
| [Int] |Random Variable|Random variable - random integer - usage example sin( 3*[Int] )|[Int]*3|3.0|
| [Int1] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^1, 10^1} - usage example sin( 3*[Int1] )|2*[Int1]|3.0|
| [Int2] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^2, 10^2} - usage example sin( 3*[Int2] )|[Int2]*3|3.0|
| [Int3] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^3, 10^3} - usage example sin( 3*[Int3] )|2*[Int3]|3.0|
| [Int4] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^4, 10^4} - usage example sin( 3*[Int4] )|[Int4]*3|3.0|
| [Int5] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^5, 10^5} - usage example sin( 3*[Int5] )|2*[Int5]|3.0|
| [Int6] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^6, 10^6} - usage example sin( 3*[Int6] )|[Int6]*3|3.0|
| [Int7] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^7, 10^7} - usage example sin( 3*[Int7] )|2*[Int7]|3.0|
| [Int8] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^8, 10^8} - usage example sin( 3*[Int8] )|[Int8]*3|3.0|
| [Int9] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^9, 10^9} - usage example sin( 3*[Int9] )|2*[Int9]|3.0|
| [nat] |Random Variable|Random variable - random natural number including 0 - usage example sin( 3*[nat] )|[nat]*3|3.0|
| [nat1] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^1} - usage example sin( 3*[nat1] )|2*[nat1]|3.0|
| [nat2] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^2} - usage example sin( 3*[nat2] )|[nat2]*3|3.0|
| [nat3] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^3} - usage example sin( 3*[nat3] )|2*[nat3]|3.0|
| [nat4] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^4} - usage example sin( 3*[nat4] )|[nat4]*3|3.0|
| [nat5] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^5} - usage example sin( 3*[nat5] )|2*[nat5]|3.0|
| [nat6] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^6} - usage example sin( 3*[nat6] )|[nat6]*3|3.0|
| [nat7] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^7} - usage example sin( 3*[nat7] )|2*[nat7]|3.0|
| [nat8] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^8} - usage example sin( 3*[nat8] )|[nat8]*3|3.0|
| [nat9] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^9} - usage example sin( 3*[nat9] )|2*[nat9]|3.0|
| [Nat] |Random Variable|Random variable - random natural number - usage example sin( 3*[Nat] )|[Nat]*3|3.0|
| [Nat1] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^1} - usage example sin( 3*[Nat1] )|2*[Nat1]|3.0|
| [Nat2] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^2} - usage example sin( 3*[Nat2] )|[Nat2]*3|3.0|
| [Nat3] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^3} - usage example sin( 3*[Nat3] )|2*[Nat3]|3.0|
| [Nat4] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^4} - usage example sin( 3*[Nat4] )|[Nat4]*3|3.0|
| [Nat5] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^5} - usage example sin( 3*[Nat5] )|2*[Nat5]|3.0|
| [Nat6] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^6} - usage example sin( 3*[Nat6] )|[Nat6]*3|3.0|
| [Nat7] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^7} - usage example sin( 3*[Nat7] )|2*[Nat7]|3.0|
| [Nat8] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^8} - usage example sin( 3*[Nat8] )|[Nat8]*3|3.0|
| [Nat9] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^9} - usage example sin( 3*[Nat9] )|2*[Nat9]|3.0|
| [Nor] |Random Variable|Random variable - Normal distribution N(0,1) - usage example cos( 3*[Nor]+1 )|[Nor]*3|3.0|
## Mathematical Constants
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| pi |Constant Value|Pi, Archimedes' constant or Ludolph's number|2*pi|1.0|
| e |Constant Value|Napier's constant, or Euler's number, base of Natural logarithm|e*3|1.0|
| [gam] |Constant Value|Euler-Mascheroni constant|2*[gam]|1.0|
| [phi] |Constant Value|Golden ratio|[phi]*3|1.0|
| [PN] |Constant Value|Plastic constant|2*[PN]|1.0|
| [B*] |Constant Value|Embree-Trefethen constant|[B*]*3|1.0|
| [F'd] |Constant Value|Feigenbaum constant alfa|2*[F'd]|1.0|
| [F'a] |Constant Value|Feigenbaum constant delta|[F'a]*3|1.0|
| [C2] |Constant Value|Twin prime constant|2*[C2]|1.0|
| [M1] |Constant Value|Meissel-Mertens constant|[M1]*3|1.0|
| [B2] |Constant Value|Brun's constant for twin primes|2*[B2]|1.0|
| [B4] |Constant Value|Brun's constant for prime quadruplets|[B4]*3|1.0|
| [BN'L] |Constant Value|De Bruijn-Newman constant|2*[BN'L]|1.0|
| [Kat] |Constant Value|Catalan's constant|[Kat]*3|1.0|
| [K*] |Constant Value|Landau-Ramanujan constant|2*[K*]|1.0|
| [K.] |Constant Value|Viswanath's constant|[K.]*3|1.0|
| [B'L] |Constant Value|Legendre's constant|2*[B'L]|1.0|
| [RS'm] |Constant Value|Ramanujan-Soldner constant|[RS'm]*3|1.0|
| [EB'e] |Constant Value|Erdos-Borwein constant|2*[EB'e]|1.0|
| [Bern] |Constant Value|Bernstein's constant|[Bern]*3|1.0|
| [GKW'l] |Constant Value|Gauss-Kuzmin-Wirsing constant|2*[GKW'l]|1.0|
| [HSM's] |Constant Value|Hafner-Sarnak-McCurley constant|[HSM's]*3|1.0|
| [lm] |Constant Value|Golomb-Dickman constant|2*[lm]|1.0|
| [Cah] |Constant Value|Cahen's constant|[Cah]*3|1.0|
| [Ll] |Constant Value|Laplace limit|2*[Ll]|1.0|
| [AG] |Constant Value|Alladi-Grinstead constant|[AG]*3|1.0|
| [L*] |Constant Value|Lengyel's constant|2*[L*]|1.0|
| [L.] |Constant Value|Levy's constant|[L.]*3|1.0|
| [Dz3] |Constant Value|Apery's constant|2*[Dz3]|1.0|
| [A3n] |Constant Value|Mills' constant|[A3n]*3|1.0|
| [Bh] |Constant Value|Backhouse's constant|2*[Bh]|1.0|
| [Pt] |Constant Value|Porter's constant|[Pt]*3|1.0|
| [L2] |Constant Value|Lieb's square ice constant|2*[L2]|1.0|
| [Nv] |Constant Value|Niven's constant|[Nv]*3|1.0|
| [Ks] |Constant Value|Sierpinski's constant|2*[Ks]|1.0|
| [Kh] |Constant Value|Khinchin's constant|[Kh]*3|1.0|
| [FR] |Constant Value|Fransen-Robinson constant|2*[FR]|1.0|
| [La] |Constant Value|Landau's constant|[La]*3|1.0|
| [P2] |Constant Value|Parabolic constant|2*[P2]|1.0|
| [Om] |Constant Value|Omega constant|[Om]*3|1.0|
| [MRB] |Constant Value|MRB constant|2*[MRB]|1.0|
| [li2] |Constant Value|li(2) - logarithmic integral function at x=2|[li2]*3|2.3|
| [EG] |Constant Value|Gompertz constant|2*[EG]|2.3|
| [true] | Constant Value | Boolean True represented as double, [true] = 1 | [true] | 4.1 |
| [false] | Constant Value | Boolean False represented as double, [false] = 0 | [false] | 4.1 |
| [NaN] | Constant Value | Not-a-Number | [NaN] | 4.1 |
## Physical Constant
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [c] |Constant Value|\ Light speed in vacuum [m/s] (m=1, s=1)|[c]*3|4.0|
| [G.] |Constant Value|\ Gravitational constant (m=1, kg=1, s=1)]|2*[G.]|4.0|
| [g] |Constant Value|\ Gravitational acceleration on Earth [m/s^2] (m=1, s=1)|[g]*3|4.0|
| [hP] |Constant Value|\ Planck constant (m=1, kg=1, s=1)|2*[hP]|4.0|
| [h-] |Constant Value|\ Reduced Planck constant / Dirac constant (m=1, kg=1, s=1)]|[h-]*3|4.0|
| [lP] |Constant Value|\ Planck length [m] (m=1)|2*[lP]|4.0|
| [mP] |Constant Value|\ Planck mass [kg] (kg=1)|[mP]*3|4.0|
| [tP] |Constant Value|\ Planck time [s] (s=1)|2*[tP]|4.0|
## Astronomical Constant
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [ly] |Constant Value|\ Light year [m] (m=1)|[ly]*3|4.0|
| [au] |Constant Value|\ Astronomical unit [m] (m=1)|2*[au]|4.0|
| [pc] |Constant Value|\ Parsec [m] (m=1)|[pc]*3|4.0|
| [kpc] |Constant Value|\ Kiloparsec [m] (m=1)|2*[kpc]|4.0|
| [Earth-R-eq] |Constant Value|\ Earth equatorial radius [m] (m=1)|[Earth-R-eq]*3|4.0|
| [Earth-R-po] |Constant Value|\ Earth polar radius [m] (m=1)|2*[Earth-R-po]|4.0|
| [Earth-R] |Constant Value|\ Earth mean radius (m=1)|[Earth-R]*3|4.0|
| [Earth-M] |Constant Value|\ Earth mass [kg] (kg=1)|2*[Earth-M]|4.0|
| [Earth-D] |Constant Value|\ Earth-Sun distance - semi major axis [m] (m=1)|[Earth-D]*3|4.0|
| [Moon-R] |Constant Value|\ Moon mean radius [m] (m=1)|2*[Moon-R]|4.0|
| [Moon-M] |Constant Value|\ Moon mass [kg] (kg=1)|[Moon-M]*3|4.0|
| [Moon-D] |Constant Value|\ Moon-Earth distance - semi major axis [m] (m=1)|2*[Moon-D]|4.0|
| [Solar-R] |Constant Value|\ Solar mean radius [m] (m=1)|[Solar-R]*3|4.0|
| [Solar-M] |Constant Value|\ Solar mass [kg] (kg=1)|2*[Solar-M]|4.0|
| [Mercury-R] |Constant Value|\ Mercury mean radius [m] (m=1)|[Mercury-R]*3|4.0|
| [Mercury-M] |Constant Value|\ Mercury mass [kg] (kg=1)|2*[Mercury-M]|4.0|
| [Mercury-D] |Constant Value|\ Mercury-Sun distance - semi major axis [m] (m=1)|[Mercury-D]*3|4.0|
| [Venus-R] |Constant Value|\ Venus mean radius [m] (m=1)|2*[Venus-R]|4.0|
| [Venus-M] |Constant Value|\ Venus mass [kg] (kg=1)|[Venus-M]*3|4.0|
| [Venus-D] |Constant Value|\ Venus-Sun distance - semi major axis [m] (m=1)|2*[Venus-D]|4.0|
| [Mars-R] |Constant Value|\ Mars mean radius [m] (m=1)|[Mars-R]*3|4.0|
| [Mars-M] |Constant Value|\ Mars mass [kg] (kg=1)|2*[Mars-M]|4.0|
| [Mars-D] |Constant Value|\ Mars-Sun distance - semi major axis [m] (m=1)|[Mars-D]*3|4.0|
| [Jupiter-R] |Constant Value|\ Jupiter mean radius [m] (m=1)|2*[Jupiter-R]|4.0|
| [Jupiter-M] |Constant Value|\ Jupiter mass [kg] (kg=1)|[Jupiter-M]*3|4.0|
| [Jupiter-D] |Constant Value|\ Jupiter-Sun distance - semi major axis [m] (m=1)|2*[Jupiter-D]|4.0|
| [Saturn-R] |Constant Value|\ Saturn mean radius [m] (m=1)|[Saturn-R]*3|4.0|
| [Saturn-M] |Constant Value|\ Saturn mass [kg] (kg=1)|2*[Saturn-M]|4.0|
| [Saturn-D] |Constant Value|\ Saturn-Sun distance - semi major axis [m] (m=1)|[Saturn-D]*3|4.0|
| [Uranus-R] |Constant Value|\ Uranus mean radius [m] (m=1)|2*[Uranus-R]|4.0|
| [Uranus-M] |Constant Value|\ Uranus mass [kg] (kg=1)|[Uranus-M]*3|4.0|
| [Uranus-D] |Constant Value|\ Uranus-Sun distance - semi major axis [m] (m=1)|2*[Uranus-D]|4.0|
| [Neptune-R] |Constant Value|\ Neptune mean radius [m] (m=1)|[Neptune-R]*3|4.0|
| [Neptune-M] |Constant Value|\ Neptune mass [kg] (kg=1)|2*[Neptune-M]|4.0|
| [Neptune-D] |Constant Value|\ Neptune-Sun distance - semi major axis [m] (m=1)|[Neptune-D]*3|4.0|
## Metric prefixes
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [%] |Unit|\ Percentage = 0.01|2*[%]|4.0|
| [%%] |Unit|\ Promil, Per mille = 0.001|[%%]*3|4.0|
| [Y] |Unit|\ Septillion / Yotta = 10^24|2*[Y]|4.0|
| [sept] |Unit|\ Septillion / Yotta = 10^24|[sept]*3|4.0|
| [Z] |Unit|\ Sextillion / Zetta = 10^21|2*[Z]|4.0|
| [sext] |Unit|\ Sextillion / Zetta = 10^21|[sext]*3|4.0|
| [E] |Unit|\ Quintillion / Exa = 10^18|2*[E]|4.0|
| [quint] |Unit|\ Quintillion / Exa = 10^18|[quint]*3|4.0|
| [P] |Unit|\ Quadrillion / Peta = 10^15|2*[P]|4.0|
| [quad] |Unit|\ Quadrillion / Peta = 10^15|[quad]*3|4.0|
| [T] |Unit|\ Trillion / Tera = 10^12|2*[T]|4.0|
| [tril] |Unit|\ Trillion / Tera = 10^12|[tril]*3|4.0|
| [G] |Unit|\ Billion / Giga = 10^9|2*[G]|4.0|
| [bil] |Unit|\ Billion / Giga = 10^9|[bil]*3|4.0|
| [M] |Unit|\ Million / Mega = 10^6|2*[M]|4.0|
| [mil] |Unit|\ Million / Mega = 10^6|[mil]*3|4.0|
| [k] |Unit|\ Thousand / Kilo = 10^3|2*[k]|4.0|
| [th] |Unit|\ Thousand / Kilo = 10^3|[th]*3|4.0|
| [hecto] |Unit|\ Hundred / Hecto = 10^2|2*[hecto]|4.0|
| [hund] |Unit|\ Hundred / Hecto = 10^2|[hund]*3|4.0|
| [deca] |Unit|\ Ten / Deca = 10|2*[deca]|4.0|
| [ten] |Unit|\ Ten / Deca = 10|[ten]*3|4.0|
| [deci] |Unit|\ Tenth / Deci = 0.1|2*[deci]|4.0|
| [centi] |Unit|\ Hundredth / Centi = 0.01|[centi]*3|4.0|
| [milli] |Unit|\ Thousandth / Milli = 0.001|2*[milli]|4.0|
| [mic] |Unit|\ Millionth / Micro = 10^-6|[mic]*3|4.0|
| [n] |Unit|\ Billionth / Nano = 10^-9|2*[n]|4.0|
| [p] |Unit|\ Trillionth / Pico = 10^-12|[p]*3|4.0|
| [f] |Unit|\ Quadrillionth / Femto = 10^-15|2*[f]|4.0|
| [a] |Unit|\ Quintillionth / Atoo = 10^-18|[a]*3|4.0|
| [z] |Unit|\ Sextillionth / Zepto = 10^-21|2*[z]|4.0|
| [y] |Unit|\ Septillionth / Yocto = 10^-24|[y]*3|4.0|
## Units of length
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m] |Unit|\ Metre / Meter (m=1)|2*[m]|4.0|
| [km] |Unit|\ Kilometre / Kilometer (m=1)|[km]*3|4.0|
| [cm] |Unit|\ Centimetre / Centimeter (m=1)|2*[cm]|4.0|
| [mm] |Unit|\ Millimetre / Millimeter (m=1)|[mm]*3|4.0|
| [inch] |Unit|\ Inch (m=1)|2*[inch]|4.0|
| [yd] |Unit|\ Yard (m=1)|[yd]*3|4.0|
| [ft] |Unit|\ Feet (m=1)|2*[ft]|4.0|
| [mile] |Unit|\ Mile (m=1)|[mile]*3|4.0|
| [nmi] |Unit|\ Nautical mile (m=1)|2*[nmi]|4.0|
## Units of area
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m2] |Unit|\ Square metre / Square meter (m=1)|[m2]*3|4.0|
| [cm2] |Unit|\ Square centimetre / Square centimeter (m=1)|2*[cm2]|4.0|
| [mm2] |Unit|\ Square millimetre / Square millimeter (m=1)|[mm2]*3|4.0|
| [are] |Unit|\ Are (m=1)|2*[are]|4.0|
| [ha] |Unit|\ Hectare (m=1)|[ha]*3|4.0|
| [acre] |Unit|\ Acre (m=1)|2*[acre]|4.0|
| [km2] |Unit|\ Square kilometre / Square kilometer (m=1)|[km2]*3|4.0|
## Units of volume
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [mm3] |Unit|\ Cubic millimetre / Cubic millimeter (m=1)|2*[mm3]|4.0|
| [cm3] |Unit|\ Cubic centimetre / Cubic centimeter (m=1)|[cm3]*3|4.0|
| [m3] |Unit|\ Cubic metre / Cubic meter (m=1)|2*[m3]|4.0|
| [km3] |Unit|\ Cubic kilometre / Cubic kilometer (m=1)|[km3]*3|4.0|
| [ml] |Unit|\ Millilitre / Milliliter (m=1)|2*[ml]|4.0|
| [l] |Unit|\ Litre / Liter (m=1)|[l]*3|4.0|
| [gall] |Unit|\ Gallon (m=1)|2*[gall]|4.0|
| [pint] |Unit|\ Pint (m=1)|[pint]*3|4.0|
## Units of time
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [s] |Unit|\ Second (s=1)|2*[s]|4.0|
| [ms] |Unit|\ Millisecond (s=1)|[ms]*3|4.0|
| [min] |Unit|\ Minute (s=1)|2*[min]|4.0|
| [h] |Unit|\ Hour (s=1)|[h]*3|4.0|
| [day] |Unit|\ Day (s=1)|2*[day]|4.0|
| [week] |Unit|\ Week (s=1)|[week]*3|4.0|
| [yearj] |Unit|\ Julian year = 365.25 days (s=1)|2*[yearj]|4.0|
## Units of mass
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [kg] |Unit|\ Kilogram (kg=1)|[kg]*3|4.0|
| [gr] |Unit|\ Gram (kg=1)|2*[gr]|4.0|
| [mg] |Unit|\ Milligram (kg=1)|[mg]*3|4.0|
| [dag] |Unit|\ Decagram (kg=1)|2*[dag]|4.0|
| [t] |Unit|\ Tonne (kg=1)|[t]*3|4.0|
| [oz] |Unit|\ Ounce (kg=1)|2*[oz]|4.0|
| [lb] |Unit|\ Pound (kg=1)|[lb]*3|4.0|
## Units of information
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [b] |Unit|\ Bit (bit=1)|2*[b]|4.0|
| [kb] |Unit|\ Kilobit (bit=1)|[kb]*3|4.0|
| [Mb] |Unit|\ Megabit (bit=1)|2*[Mb]|4.0|
| [Gb] |Unit|\ Gigabit (bit=1)|[Gb]*3|4.0|
| [Tb] |Unit|\ Terabit (bit=1)|2*[Tb]|4.0|
| [Pb] |Unit|\ Petabit (bit=1)|[Pb]*3|4.0|
| [Eb] |Unit|\ Exabit (bit=1)|2*[Eb]|4.0|
| [Zb] |Unit|\ Zettabit (bit=1)|[Zb]*3|4.0|
| [Yb] |Unit|\ Yottabit (bit=1)|2*[Yb]|4.0|
| [B] |Unit|\ Byte (bit=1)|[B]*3|4.0|
| [kB] |Unit|\ Kilobyte (bit=1)|2*[kB]|4.0|
| [MB] |Unit|\ Megabyte (bit=1)|[MB]*3|4.0|
| [GB] |Unit|\ Gigabyte (bit=1)|2*[GB]|4.0|
| [TB] |Unit|\ Terabyte (bit=1)|[TB]*3|4.0|
| [PB] |Unit|\ Petabyte (bit=1)|2*[PB]|4.0|
| [EB] |Unit|\ Exabyte (bit=1)|[EB]*3|4.0|
| [ZB] |Unit|\ Zettabyte (bit=1)|2*[ZB]|4.0|
| [YB] |Unit|\ Yottabyte (bit=1)|[YB]*3|4.0|
## Units of energy
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [J] |Unit|\ Joule (m=1, kg=1, s=1)|2*[J]|4.0|
| [eV] |Unit|\ Electronovolt (m=1, kg=1, s=1)|[eV]*3|4.0|
| [keV] |Unit|\ Kiloelectronovolt (m=1, kg=1, s=1)|2*[keV]|4.0|
| [MeV] |Unit|\ Megaelectronovolt (m=1, kg=1, s=1)|[MeV]*3|4.0|
| [GeV] |Unit|\ Gigaelectronovolt (m=1, kg=1, s=1)|2*[GeV]|4.0|
| [TeV] |Unit|\ Teraelectronovolt (m=1, kg=1, s=1)|[TeV]*3|4.0|
## Units of speed
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m/s] |Unit|\ Metre / Meter per second (m=1, s=1)|2*[m/s]|4.0|
| [km/h] |Unit|\ Kilometre / Kilometer per hour (m=1, s=1)|[km/h]*3|4.0|
| [mi/h] |Unit|\ Mile per hour (m=1, s=1)|2*[mi/h]|4.0|
| [knot] |Unit|\ Knot (m=1, s=1)|[knot]*3|4.0|
## Units of acceleration
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m/s2] |Unit|\ Metre / Meter per square second (m=1, s=1)|2*[m/s2]|4.0|
| [km/h2] |Unit|\ Kilometre / Kilometer per square hour (m=1, s=1)|[km/h2]*3|4.0|
| [mi/h2] |Unit|\ Mile per square hour (m=1, s=1)|2*[mi/h2]|4.0|
## Units of angle
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [rad] |Unit|\ Radian (rad=1)|[rad]*pi|4.0|
| [deg] |Unit|\ Degree of arc (rad=1)|180*[deg]|4.0|
| ['] |Unit|\ Minute of arc (rad=1)|[']*3|4.0|
| [''] |Unit|\ Second of arc (rad=1)|2*['']|4.0|
## Other parser symbols
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| ( |Parser Symbol|Left parentheses|(3+2)/4|1.0|
| ) |Parser Symbol|Right parentheses|(3+2)/4|1.0|
| , |Parser Symbol|Comma (function parameters)|min(2,3,1)|1.0|
| ; |Parser Symbol|Semicolon (function parameters)|min(2;3;1)|1.0|
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# Enjoy :-)
Best regards,
*Mariusz Gromada*
](https://play.google.com/store/apps/details?id=org.mathparser.scalar.pro&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
# MathParser.org-mXparser


# mXparser - optional donation
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser - a super easy, rich and highly flexible Mathematical Expression Parser (Math Parser, Expression Evaluator) library for JAVA, Android and C# .NET.
### 15.10.2020: first 500000 downloads!
### 20.12.2019: first 250000 downloads!
### 01.01.2019: first 100000 downloads!
### 01.08.2018: first 60000 downloads!
### 20.11.2017: first 20000 downloads!
### 01.09.2017: first 15000 downloads!
### 04.05.2017: first 10000 downloads!
### 31.03.2016: first 1000 downloads!

**mXparser** is **a highly flexible parser of mathematical expressions provided as text**. Software delivers easy to use API for JAVA and C# .NET.
# Supported frameworks

- JAVA: 6+
- Android - tested with mxparser compiled using jdk 1.7
- .NET Framework (2+) / MONO CLS
- .NET Core: 1+
- .NET Standard: 1+
- .NET PCL
- Xamarin

# JAVA intro

# C# intro

# Tutorial

# [>>> Click to learn from examples <<<](http://mathparser.org/mxparser-tutorial/)
# Main functionalities:
- **basic operators**, i.e.: +, -, *, ^, !
- **[Boolean logic](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BooleanAlgebra.html)** operators i.e.: or, and, xor
- **[binary relations](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BinaryRelations.html)** i.e.: =, <, >
- **[math functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html)** (large library of 1-arg, 2-arg, 3-arg - functions) i.e.: sin, cos, Stirling numbers, log, inverse functions
- **[constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathConstants.html)** (large library), i.e.: pi, e, golden ratio
- **n-args functions**, i.e.: [greatest common divisor](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html#gcd-int...-)
- **[iterated summation and product operators](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumberTheory.html#sigmaSummation-org.mariuszgromada.math.mxparser.Expression-org.mariuszgromada.math.mxparser.Argument-double-double-double-)**
- **[differentiation and integration](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumericalAnalysis.html)**
# High flexibility functionalities
- **[user defined constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Constant.html)** and arguments, both free - and dependent on other arguments + possibility of use in functions
- **[user defined functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html)** (both free and depended)
- **[user defined recursive arguments](http://mathparser.org/api/org/mariuszgromada/math/mxparser/RecursiveArgument.html)** + simple (controlled) recursion (1 recursive argument)
- **[user defined recursive functions / expressions (any)](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html#getRecursiveMode--)** - complex, many arguments, no limitation
- **[internal syntax checking](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#checkSyntax--)**
- **[internal help](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getHelp--)**
- other useful functionalities, i.e.: [computing time](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getComputingTime--), expression description.
# Project documentation
### - [mXparser - API (english)](http://mathparser.org/api/)
### - [mXparser - WIKI (english)](https://github.com/mariuszgromada/MathParser.org-mXparser/wiki)
### - [mXparser - Tutorial (english)](http://mathparser.org/mxparser-tutorial/)
### - [MathSpace.pl - site about math with mXparser examples (polish)](http://mathspace.pl/)
### - [MathParser.org - site about mXparser (english)](http://mathparser.org/)
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser in nutshell
#### You want simple calculator...
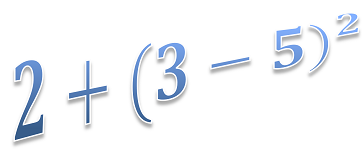
Expression e = new Expression("2+3");
e.calculate();
:+1:
#### A calculator supporting parenthesis...

Expression e = new Expression("2+(3-5)^2");
e.calculate();
:+1:
#### You care about predefined constants...

Expression e = new Expression("2*pi");
e.calculate();
:+1:
#### You need to define your own constants...
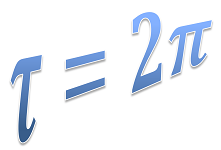
Constant tau = new Constant("tau = 2*pi");
Expression e = new Expression("3*tau", tau);
e.calculate();
:+1:
#### You enjoy using many built-in functions...

Expression e = new Expression("sin(2*pi)");
e.calculate();
:+1:
#### You do not limit yourself to unary functions...
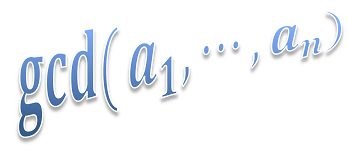
Expression e = new Expression("gcd(2,5,10,30)");
e.calculate();
:+1:
#### What about user defined arguments...
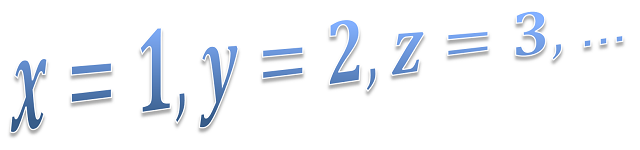
Argument x = new Argument("x = 5");
Expression e = new Expression("sin(x)");
e.calculate();
:+1:
#### You are considering dependent arguments...

Argument x = new Argument("x = 5");
Argument y = new Argument("y = 2*x", x);
Expression e = new Expression("sin(y)", y);
e.calculate();
:+1:
#### You need to apply some logic...

Argument x = new Argument("x = 5");
Expression e = new Expression("if(sin(x) > 5, 1, 0)", x);
e.calculate();
:+1:
#### Yes, you are right, there is a support for Boolean algebra!

Expression e = new Expression("5=6");
e.calculate();
:+1:
#### And for binary relations as well!
Expression e = new Expression("5 <= 6");
e.calculate();
:+1:
## mXparser is cool! But this is only the begging, we are just warming up!
#### You want to play with iterated operators...

Expression e = new Expression("sum(i, 1, 10, 2*i^2 + pi)");
e.calculate();
:+1:
#### You want to iterate differently by not necessarily whole numbes...

Expression e = new Expression("prod(i, 1, 5, i, 0.5)");
e.calculate();
:+1:
#### You want to have more fun with math...
Argument x = new Argument("x = pi/2");
Expression e20 = new Expression("sum(n,0,10,(-1)^n*(x^(2*n+1))/(2*n+1)!)", x);
e.calculate();
:+1:
#### You still want more fun with calculus operations, i.e. differentiation...
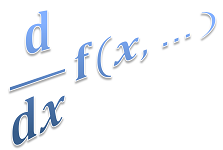
Argument x = new Argument("x = pi/2");
Expression e = new Expression("cos(x)-der(sin(x), x)", x);
e.calculate();
:+1:
#### And definite integrals as well...
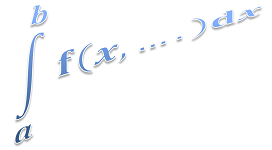
Expression e = new Expression("2*int(sqrt(1-x^2), x, -1, 1)");
e.calculate();
:+1:
## mXparser is even cooler! It is time to ask about ...
#### user defined functions...
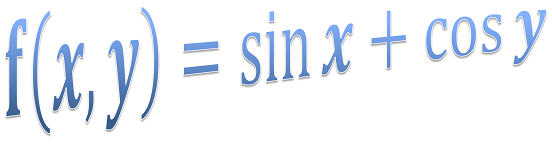
Function f = new Function("f(x,y) = sin(x) + cos(y)");
f.calculate(1,2);
Expression e = new Expression("f(1,2) - 10", f);
e.calculate();
:+1:
#### Recursion is your desire...
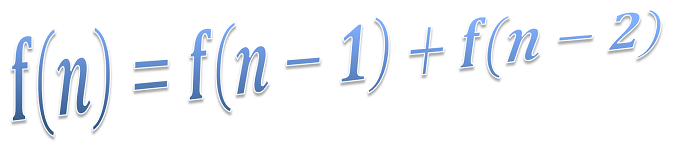
Function f = new Function("f(n) = if( n>0, n*f(n-1), 1)");
f.calculate()
:+1:
#### Any kind of recursion...
Function Cnk = new Function("Cnk(n,k) = if(k>0, if(k |Boolean Operator|Implication (IMP)|p --> q|1.0|
| <-- |Boolean Operator|Converse implication (CIMP)|p <-- q|1.0|
| -/> |Boolean Operator|Material nonimplication (NIMP)|p -/> q|1.0|
| |Boolean Operator|Logical biconditional (EQV)|p <-> q|1.0|
| ~ |Boolean Operator|Negation|~p|1.0|
## Bitwise Operators
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| @~ |Bitwise Operator|Bitwise unary complement|@~10|4.0|
| @& |Bitwise Operator|Bitwise AND|10 @& 2|4.0|
| @^ |Bitwise Operator|Bitwise exclusive OR|10 @^ 2|4.0|
| @\| |Bitwise Operator|Bitwise inclusive OR|10 @\| 2|4.0|
| @<< |Bitwise Operator|Signed left shift|10 @<< 2|4.0|
| @>> |Bitwise Operator|Signed right shift|10 @>> 2|4.0|
## Binary Relations
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| = |Binary Relation|Equality|a = b|1.0|
| == |Binary Relation|Equality|a == b|1.0|
| <> |Binary Relation|Inequation|a <> b|1.0|
| ~= |Binary Relation|Inequation|a ~= b|1.0|
| != |Binary Relation|Inequation|a != b|1.0|
| < |Binary Relation|Lower than|a < b|1.0|
| > |Binary Relation|Greater than|a > b|1.0|
| <= |Binary Relation|Lower or equal|a <= b|1.0|
| >= |Binary Relation|Greater or equal|a >= b|1.0|
## Unary Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| sin | Unary Function | Trigonometric sine function | sin(x) | 1.0 |
| cos | Unary Function | Trigonometric cosine function | cos(x) | 1.0 |
| tg | Unary Function | Trigonometric tangent function | tg(x) | 1.0 |
| tan | Unary Function | Trigonometric tangent function | tan(x) | 1.0 |
| ctg | Unary Function | Trigonometric cotangent function | ctg(x) | 1.0 |
| cot | Unary Function | Trigonometric cotangent function | cot(x) | 1.0 |
| ctan | Unary Function | Trigonometric cotangent function | ctan(x) | 1.0 |
| sec | Unary Function | Trigonometric secant function | sec(x) | 1.0 |
| csc | Unary Function | Trigonometric cosecant function | csc(x) | 1.0 |
| cosec | Unary Function | Trigonometric cosecant function | cosec(x) | 1.0 |
| asin | Unary Function | Inverse trigonometric sine function | asin(x) | 1.0 |
| arsin | Unary Function | Inverse trigonometric sine function | arsin(x) | 1.0 |
| arcsin | Unary Function | Inverse trigonometric sine function | arcsin(x) | 1.0 |
| acos | Unary Function | Inverse trigonometric cosine function | acos(x) | 1.0 |
| arcos | Unary Function | Inverse trigonometric cosine function | arcos(x) | 1.0 |
| arccos | Unary Function | Inverse trigonometric cosine function | arccos(x) | 1.0 |
| atg | Unary Function | Inverse trigonometric tangent function | atg(x) | 1.0 |
| atan | Unary Function | Inverse trigonometric tangent function | atan(x) | 1.0 |
| arctg | Unary Function | Inverse trigonometric tangent function | arctg(x) | 1.0 |
| arctan | Unary Function | Inverse trigonometric tangent function | arctan(x) | 1.0 |
| actg | Unary Function | Inverse trigonometric cotangent function | actg(x) | 1.0 |
| acot | Unary Function | Inverse trigonometric cotangent function | acot(x) | 1.0 |
| actan | Unary Function | Inverse trigonometric cotangent function | actan(x) | 1.0 |
| arcctg | Unary Function | Inverse trigonometric cotangent function | arcctg(x) | 1.0 |
| arccot | Unary Function | Inverse trigonometric cotangent function | arccot(x) | 1.0 |
| arcctan | Unary Function | Inverse trigonometric cotangent function | arcctan(x) | 1.0 |
| ln | Unary Function | Natural logarithm function (base e) | ln(x) | 1.0 |
| log2 | Unary Function | Binary logarithm function (base 2) | log2(x) | 1.0 |
| log10 | Unary Function | Common logarithm function (base 10) | log10(x) | 1.0 |
| rad | Unary Function | Degrees to radians function | rad(x) | 1.0 |
| exp | Unary Function | Exponential function | exp(x) | 1.0 |
| sqrt | Unary Function | Squre root function | sqrt(x) | 1.0 |
| sinh | Unary Function | Hyperbolic sine function | sinh(x) | 1.0 |
| cosh | Unary Function | Hyperbolic cosine function | cosh(x) | 1.0 |
| tgh | Unary Function | Hyperbolic tangent function | tgh(x) | 1.0 |
| tanh | Unary Function | Hyperbolic tangent function | tanh(x) | 1.0 |
| coth | Unary Function | Hyperbolic cotangent function | coth(x) | 1.0 |
| ctgh | Unary Function | Hyperbolic cotangent function | ctgh(x) | 1.0 |
| ctanh | Unary Function | Hyperbolic cotangent function | ctanh(x) | 1.0 |
| sech | Unary Function | Hyperbolic secant function | sech(x) | 1.0 |
| csch | Unary Function | Hyperbolic cosecant function | csch(x) | 1.0 |
| cosech | Unary Function | Hyperbolic cosecant function | cosech(x) | 1.0 |
| deg | Unary Function | Radians to degrees function | deg(x) | 1.0 |
| abs | Unary Function | Absolut value function | abs(x) | 1.0 |
| sgn | Unary Function | Signum function | sgn(x) | 1.0 |
| floor | Unary Function | Floor function | floor(x) | 1.0 |
| ceil | Unary Function | Ceiling function | ceil(x) | 1.0 |
| not | Unary Function | Negation function | not(x) | 1.0 |
| asinh | Unary Function | Inverse hyperbolic sine function | asinh(x) | 1.0 |
| arsinh | Unary Function | Inverse hyperbolic sine function | arsinh(x) | 1.0 |
| arcsinh | Unary Function | Inverse hyperbolic sine function | arcsinh(x) | 1.0 |
| acosh | Unary Function | Inverse hyperbolic cosine function | acosh(x) | 1.0 |
| arcosh | Unary Function | Inverse hyperbolic cosine function | arcosh(x) | 1.0 |
| arccosh | Unary Function | Inverse hyperbolic cosine function | arccosh(x) | 1.0 |
| atgh | Unary Function | Inverse hyperbolic tangent function | atgh(x) | 1.0 |
| atanh | Unary Function | Inverse hyperbolic tangent function | atanh(x) | 1.0 |
| arctgh | Unary Function | Inverse hyperbolic tangent function | arctgh(x) | 1.0 |
| arctanh | Unary Function | Inverse hyperbolic tangent function | arctanh(x) | 1.0 |
| acoth | Unary Function | Inverse hyperbolic cotangent function | acoth(x) | 1.0 |
| actgh | Unary Function | Inverse hyperbolic cotangent function | actgh(x) | 1.0 |
| actanh | Unary Function | Inverse hyperbolic cotangent function | actanh(x) | 1.0 |
| arcoth | Unary Function | Inverse hyperbolic cotangent function | arcoth(x) | 1.0 |
| arccoth | Unary Function | Inverse hyperbolic cotangent function | arccoth(x) | 1.0 |
| arcctgh | Unary Function | Inverse hyperbolic cotangent function | arcctgh(x) | 1.0 |
| arcctanh | Unary Function | Inverse hyperbolic cotangent function | arcctanh(x) | 1.0 |
| asech | Unary Function | Inverse hyperbolic secant function | asech(x) | 1.0 |
| arsech | Unary Function | Inverse hyperbolic secant function | arsech(x) | 1.0 |
| arcsech | Unary Function | Inverse hyperbolic secant function | arcsech(x) | 1.0 |
| acsch | Unary Function | Inverse hyperbolic cosecant function | acsch(x) | 1.0 |
| arcsch | Unary Function | Inverse hyperbolic cosecant function | arcsch(x) | 1.0 |
| arccsch | Unary Function | Inverse hyperbolic cosecant function | arccsch(x) | 1.0 |
| acosech | Unary Function | Inverse hyperbolic cosecant function | acosech(x) | 1.0 |
| arcosech | Unary Function | Inverse hyperbolic cosecant function | arcosech(x) | 1.0 |
| Sa | Unary Function | Sinc function (normalized) | Sa(x) | 1.0 |
| sinc | Unary Function | Sinc function (normalized) | sinc(x) | 1.0 |
| Sinc | Unary Function | Sinc function (unnormalized) | Sinc(x) | 1.0 |
| Bell | Unary Function | Bell number | Bell(n) | 1.0 |
| Luc | Unary Function | Lucas number | Luc(n) | 1.0 |
| Fib | Unary Function | Fibonacci number | Fib(n) | 1.0 |
| harm | Unary Function | Harmonic number | harm(n) | 1.0 |
| ispr | Unary Function | Prime number test (is number a prime?) | ispr(n) | 2.3 |
| Pi | Unary Function | Prime-counting function - Pi(x) | Pi(n) | 2.3 |
| Ei | Unary Function | Exponential integral function (non-elementary special function) - usage example: Ei(x) | Ei(x) | 2.3 |
| li | Unary Function | Logarithmic integral function (non-elementary special function) - usage example: li(x) | li(x) | 2.3 |
| Li | Unary Function | Offset logarithmic integral function (non-elementary special function) - usage example: Li(x) | Li(x) | 2.3 |
| erf | Unary Function | Gauss error function (non-elementary special function) - usage example: 2 + erf(x) | erf(x) | 3.0 |
| erfc | Unary Function | Gauss complementary error function (non-elementary special function) - usage example: 1 - erfc(x) | erfc(x) | 3.0 |
| erfInv | Unary Function | Inverse Gauss error function (non-elementary special function) - usage example: erfInv(x) | erfInv(x) | 3.0 |
| erfcInv | Unary Function | Inverse Gauss complementary error function (non-elementary special function) - usage example: erfcInv(x) | erfcInv(x) | 3.0 |
| ulp | Unary Function | Unit in The Last Place - ulp(0.1) | ulp(x) | 3.0 |
| isNaN | Unary Function | Returns true = 1 if value is a Not-a-Number (NaN), false = 0 otherwise - usage example: isNaN(x) | isNaN(x) | 4.1 |
| ndig10 | Unary Function | Number of digits in numeral system with base 10 | ndig10(x) | 4.1 |
| nfact | Unary Function | Prime decomposition - number of distinct prime factors | nfact(x) | 4.1 |
| arcsec | Unary Function | Inverse trigonometric secant | arcsec(x) | 4.1 |
| Gamma | Unary Function | Gamma special function Γ(s) | Gamma(x) | 4.3 |
| LambW0(x) | Unary Function | Lambert-W special function, principal branch 0, also called the omega function or product logarithm | LambW0(x) | 4.3 |
| LambW1(x) | Unary Function | Lambert-W special function, branch -1, also called the omega function or product logarithm | LambW1(x) | 4.3 |
| sgnGamma | Unary Function | Signum of Gamma special function, Γ(x) | sgnGamma(x) | 4.3 |
| logGamma | Unary Function | Log Gamma special function, lnΓ(x) | logGamma(x) | 4.3 |
| diGamma | Unary Function | Digamma function as the logarithmic derivative of the Gamma special function, ψ(x) | diGamma(x) | 4.3 |
## Binary Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| log | Binary Function | Logarithm function | log(a, b) | 1.0 |
| mod | Binary Function | Modulo function | mod(a, b) | 1.0 |
| C | Binary Function | Binomial coefficient function | C(n, k) | 1.0 |
| Bern | Binary Function | Bernoulli numbers | Bern(m, n) | 1.0 |
| Stirl1 | Binary Function | Stirling numbers of the first kind | Stirl1(n, k) | 1.0 |
| Stirl2 | Binary Function | Stirling numbers of the second kind | Stirl2(n, k) | 1.0 |
| Worp | Binary Function | Worpitzky number | Worp(n, k) | 1.0 |
| Euler | Binary Function | Euler number | Euler(n, k) | 1.0 |
| KDelta | Binary Function | Kronecker delta | KDelta(i, j) | 1.0 |
| EulerPol | Binary Function | EulerPol | EulerPol | 1.0 |
| Harm | Binary Function | Harmonic number | Harm(x, n) | 1.0 |
| rUni | Binary Function | Random variable - Uniform continuous distribution U(a,b), usage example: 2*rUni(2,10) | rUni(a, b) | 3.0 |
| rUnid | Binary Function | Random variable - Uniform discrete distribution U{a,b}, usage example: 2*rUnid(2,100) | rUnid(a, b) | 3.0 |
| round | Binary Function | Half-up rounding, usage examples: round(2.2, 0) = 2, round(2.6, 0) = 3, round(2.66,1) = 2.7 | round(x, n) | 3.0 |
| rNor | Binary Function | Random variable - Normal distribution N(m,s) m - mean, s - stddev, usage example: 3*rNor(0,1) | rNor(mean, stdv) | 3.0 |
| ndig | Binary Function | Number of digits representing the number in numeral system with given base | ndig(number, base) | 4.1 |
| dig10 | Binary Function | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - base 10 numeral system | dig10(num, pos) | 4.1 |
| factval | Binary Function | Prime decomposition - factor value at position between 1 ... nfact(n) - ascending order by factor value | factval(number, factorid) | 4.1 |
| factexp | Binary Function | Prime decomposition - factor exponent / multiplicity at position between 1 ... nfact(n) - ascending order by factor value | factexp(number, factorid) | 4.1 |
| root | Binary Function | N-th order root of a number | root(rootorder, number) | 4.1 |
| GammaL | Binary Function | Lower incomplete gamma special function, γ(s,x) | GammaL(s,x) | 4.3 |
| GammaU | Binary Function | Upper incomplete Gamma special function, Γ(s,x) | GammaU(s,x) | 4.3 |
| GammaP | Binary Function | Lower regularized P gamma special function, P(s,x) | GammaP(s,x) | 4.3 |
| GammaRegL | Binary Function | Lower regularized P gamma special function, P(s,x) | GammaRegL(s,x) | 4.3 |
| GammaQ | Binary Function | Upper regularized Q Gamma special function, Q(s,x) | GammaQ(s,x) | 4.3 |
| GammaRegU | Binary Function | Upper regularized Q Gamma special function, Q(s,x) | GammaRegU(s,x) | 4.3 |
| Beta | Binary Function | The Beta special function B(x,y), also called the Euler integral of the first kind | Beta(x,y) | 4.3 |
| logBeta | Binary Function | The Log Beta special function ln B(x,y), also called the Log Euler integral of the first kind, ln B(x,y) | logBeta(x,y) | 4.3 |
## 3-args Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| if | 3-args Function | If function | if( cond, expr-if-true, expr-if-false ) | 1.0 |
| chi | 3-args Function | Characteristic function for x in (a,b) | chi(x, a, b) | 1.0 |
| CHi | 3-args Function | Characteristic function for x in [a,b] | CHi(x, a, b) | 1.0 |
| Chi | 3-args Function | Characteristic function for x in [a,b) | Chi(x, a, b) | 1.0 |
| cHi | 3-args Function | Characteristic function for x in (a,b] | cHi(x, a, b) | 1.0 |
| pUni | 3-args Function | Probability distribution function - Uniform continuous distribution U(a,b) | pUni(x, a, b) | 3.0 |
| cUni | 3-args Function | Cumulative distribution function - Uniform continuous distribution U(a,b) | cUni(x, a, b) | 3.0 |
| qUni | 3-args Function | Quantile function (inverse cumulative distribution function) - Uniform continuous distribution U(a,b) | qUni(q, a, b) | 3.0 |
| pNor | 3-args Function | Probability distribution function - Normal distribution N(m,s) | pNor(x, mean, stdv) | 3.0 |
| cNor | 3-args Function | Cumulative distribution function - Normal distribution N(m,s) | cNor(x, mean, stdv) | 3.0 |
| qNor | 3-args Function | Quantile function (inverse cumulative distribution function) | qNor(q, mean, stdv) | 3.0 |
| dig | 3-args Function | Digit at position 1 ... n (left -> right) or 0 ... -(n-1) (right -> left) - numeral system with given base | dig(num, pos, base) | 4.1 |
| BetaInc | 3-args Function | The incomplete beta special function B(x; a, b), also called the incomplete Euler integral of the first kind | BetaInc(x,a,b) | 4.3 |
| BetaI | 3-args Function | The regularized incomplete beta (or regularized beta) special function I(x; a, b), also called the regularized incomplete Euler integral of the first kind | BetaI(x,a,b) | 4.3 |
| BetaReg | 3-args Function | The regularized incomplete beta (or regularized beta) special function I(x; a, b), also called the regularized incomplete Euler integral of the first kind | BetaReg(x,a,b) | 4.3 |
## Variadic Functions
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| iff | Variadic Function | If function | iff( cond-1, expr-1; ... ; cond-n, expr-n ) | 1.0 |
| min | Variadic Function | Minimum function | min(a1, ..., an) | 1.0 |
| max | Variadic Function | Maximum function | max(a1, ..., an) | 1.0 |
| ConFrac | Variadic Function | Continued fraction | ConFrac(a1, ..., an) | 1.0 |
| ConPol | Variadic Function | Continued polynomial | ConPol(a1, ..., an) | 1.0 |
| gcd | Variadic Function | Greatest common divisor | gcd(a1, ..., an) | 1.0 |
| lcm | Variadic Function | Least common multiple | lcm(a1, ..., an) | 1.0 |
| add | Variadic Function | Summation operator | add(a1, ..., an) | 2.4 |
| multi | Variadic Function | Multiplication | multi(a1, ..., an) | 2.4 |
| mean | Variadic Function | Mean / average value | mean(a1, ..., an) | 2.4 |
| var | Variadic Function | Bias-corrected sample variance | var(a1, ..., an) | 2.4 |
| std | Variadic Function | Bias-corrected sample standard deviation | std(a1, ..., an) | 2.4 |
| rList | Variadic Function | Random number from given list of numbers | rList(a1, ..., an) | 3.0 |
| coalesce | Variadic Function | Returns the first non-NaN value | coalesce(a1, ..., an) | 4.1 |
| or | Variadic Function | Logical disjunction (OR) - variadic | or(a1, ..., an) | 4.1 |
| and | Variadic Function | Logical conjunction (AND) - variadic | and(a1, ..., an) | 4.1 |
| xor | Variadic Function | Exclusive or (XOR) - variadic | xor(a1, ..., an) | 4.1 |
| argmin | Variadic Function | Arguments / indices of the minima | argmin(a1, ..., an) | 4.1 |
| argmax | Variadic Function | Arguments / indices of the maxima | argmax(a1, ..., an) | 4.1 |
| med | Variadic Function | The sample median | med(a1, ..., an) | 4.1 |
| mode | Variadic Function | Mode - the value that appears most often | mode(a1, ..., an) | 4.1 |
| base | Variadic Function | Returns number in given numeral system base represented by list of digits | base(b, d1, ..., dn) | 4.1 |
| ndist | Variadic Function | Number of distinct values | ndist(v1, ..., vn) | 4.1 |
## Calculus Operators / Iterated Operators
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| sum | Calculus Operator | Summation operator - SIGMA | sum( i, from, to, expr , ) | 1.0 |
| prod | Calculus Operator | Product operator - PI | prod( i, from, to, expr , ) | 1.0 |
| int | Calculus Operator | Definite integral operator | int( expr, arg, from, to ) | 1.0 |
| der | Calculus Operator | Derivative operator | der( expr, arg, ) | 1.0 |
| der- | Calculus Operator | Left derivative operator | der-( expr, arg, ) | 1.0 |
| der+ | Calculus Operator | Right derivative operator | der+( expr, arg, ) | 1.0 |
| dern | Calculus Operator | n-th derivative operator | dern( expr, n, arg ) | 1.0 |
| diff | Calculus Operator | Forward difference operator | diff( expr, arg, ) | 1.0 |
| difb | Calculus Operator | Backward difference operator | difb( expr, arg, ) | 1.0 |
| avg | Calculus Operator | Average operator | avg( i, from, to, expr , ) | 2.4 |
| vari | Calculus Operator | Bias-corrected sample variance operator | vari( i, from, to, expr , ) | 2.4 |
| stdi | Calculus Operator | Bias-corrected sample standard deviation operator | stdi( i, from, to, expr , ) | 2.4 |
| mini | Calculus Operator | Minimum value | mini( i, from, to, expr , ) | 2.4 |
| maxi | Calculus Operator | Maximum value | maxi( i, from, to, expr , ) | 2.4 |
| solve | Calculus Operator | f(x) = 0 equation solving, function root finding | solve( expr, a, b ) | 4.0 |
## Random Variables
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [Uni] |Random Variable|Random variable - Uniform continuous distribution U(0,1), usage example: 2*[Uni]|2*[Uni]|3.0|
| [Int] |Random Variable|Random variable - random integer - usage example sin( 3*[Int] )|[Int]*3|3.0|
| [Int1] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^1, 10^1} - usage example sin( 3*[Int1] )|2*[Int1]|3.0|
| [Int2] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^2, 10^2} - usage example sin( 3*[Int2] )|[Int2]*3|3.0|
| [Int3] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^3, 10^3} - usage example sin( 3*[Int3] )|2*[Int3]|3.0|
| [Int4] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^4, 10^4} - usage example sin( 3*[Int4] )|[Int4]*3|3.0|
| [Int5] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^5, 10^5} - usage example sin( 3*[Int5] )|2*[Int5]|3.0|
| [Int6] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^6, 10^6} - usage example sin( 3*[Int6] )|[Int6]*3|3.0|
| [Int7] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^7, 10^7} - usage example sin( 3*[Int7] )|2*[Int7]|3.0|
| [Int8] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^8, 10^8} - usage example sin( 3*[Int8] )|[Int8]*3|3.0|
| [Int9] |Random Variable|Random variable - random integer - Uniform discrete distribution U{-10^9, 10^9} - usage example sin( 3*[Int9] )|2*[Int9]|3.0|
| [nat] |Random Variable|Random variable - random natural number including 0 - usage example sin( 3*[nat] )|[nat]*3|3.0|
| [nat1] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^1} - usage example sin( 3*[nat1] )|2*[nat1]|3.0|
| [nat2] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^2} - usage example sin( 3*[nat2] )|[nat2]*3|3.0|
| [nat3] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^3} - usage example sin( 3*[nat3] )|2*[nat3]|3.0|
| [nat4] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^4} - usage example sin( 3*[nat4] )|[nat4]*3|3.0|
| [nat5] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^5} - usage example sin( 3*[nat5] )|2*[nat5]|3.0|
| [nat6] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^6} - usage example sin( 3*[nat6] )|[nat6]*3|3.0|
| [nat7] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^7} - usage example sin( 3*[nat7] )|2*[nat7]|3.0|
| [nat8] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^8} - usage example sin( 3*[nat8] )|[nat8]*3|3.0|
| [nat9] |Random Variable|Random variable - random natural number including 0 - Uniform discrete distribution U{0, 10^9} - usage example sin( 3*[nat9] )|2*[nat9]|3.0|
| [Nat] |Random Variable|Random variable - random natural number - usage example sin( 3*[Nat] )|[Nat]*3|3.0|
| [Nat1] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^1} - usage example sin( 3*[Nat1] )|2*[Nat1]|3.0|
| [Nat2] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^2} - usage example sin( 3*[Nat2] )|[Nat2]*3|3.0|
| [Nat3] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^3} - usage example sin( 3*[Nat3] )|2*[Nat3]|3.0|
| [Nat4] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^4} - usage example sin( 3*[Nat4] )|[Nat4]*3|3.0|
| [Nat5] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^5} - usage example sin( 3*[Nat5] )|2*[Nat5]|3.0|
| [Nat6] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^6} - usage example sin( 3*[Nat6] )|[Nat6]*3|3.0|
| [Nat7] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^7} - usage example sin( 3*[Nat7] )|2*[Nat7]|3.0|
| [Nat8] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^8} - usage example sin( 3*[Nat8] )|[Nat8]*3|3.0|
| [Nat9] |Random Variable|Random variable - random natural number - Uniform discrete distribution U{1, 10^9} - usage example sin( 3*[Nat9] )|2*[Nat9]|3.0|
| [Nor] |Random Variable|Random variable - Normal distribution N(0,1) - usage example cos( 3*[Nor]+1 )|[Nor]*3|3.0|
## Mathematical Constants
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| pi |Constant Value|Pi, Archimedes' constant or Ludolph's number|2*pi|1.0|
| e |Constant Value|Napier's constant, or Euler's number, base of Natural logarithm|e*3|1.0|
| [gam] |Constant Value|Euler-Mascheroni constant|2*[gam]|1.0|
| [phi] |Constant Value|Golden ratio|[phi]*3|1.0|
| [PN] |Constant Value|Plastic constant|2*[PN]|1.0|
| [B*] |Constant Value|Embree-Trefethen constant|[B*]*3|1.0|
| [F'd] |Constant Value|Feigenbaum constant alfa|2*[F'd]|1.0|
| [F'a] |Constant Value|Feigenbaum constant delta|[F'a]*3|1.0|
| [C2] |Constant Value|Twin prime constant|2*[C2]|1.0|
| [M1] |Constant Value|Meissel-Mertens constant|[M1]*3|1.0|
| [B2] |Constant Value|Brun's constant for twin primes|2*[B2]|1.0|
| [B4] |Constant Value|Brun's constant for prime quadruplets|[B4]*3|1.0|
| [BN'L] |Constant Value|De Bruijn-Newman constant|2*[BN'L]|1.0|
| [Kat] |Constant Value|Catalan's constant|[Kat]*3|1.0|
| [K*] |Constant Value|Landau-Ramanujan constant|2*[K*]|1.0|
| [K.] |Constant Value|Viswanath's constant|[K.]*3|1.0|
| [B'L] |Constant Value|Legendre's constant|2*[B'L]|1.0|
| [RS'm] |Constant Value|Ramanujan-Soldner constant|[RS'm]*3|1.0|
| [EB'e] |Constant Value|Erdos-Borwein constant|2*[EB'e]|1.0|
| [Bern] |Constant Value|Bernstein's constant|[Bern]*3|1.0|
| [GKW'l] |Constant Value|Gauss-Kuzmin-Wirsing constant|2*[GKW'l]|1.0|
| [HSM's] |Constant Value|Hafner-Sarnak-McCurley constant|[HSM's]*3|1.0|
| [lm] |Constant Value|Golomb-Dickman constant|2*[lm]|1.0|
| [Cah] |Constant Value|Cahen's constant|[Cah]*3|1.0|
| [Ll] |Constant Value|Laplace limit|2*[Ll]|1.0|
| [AG] |Constant Value|Alladi-Grinstead constant|[AG]*3|1.0|
| [L*] |Constant Value|Lengyel's constant|2*[L*]|1.0|
| [L.] |Constant Value|Levy's constant|[L.]*3|1.0|
| [Dz3] |Constant Value|Apery's constant|2*[Dz3]|1.0|
| [A3n] |Constant Value|Mills' constant|[A3n]*3|1.0|
| [Bh] |Constant Value|Backhouse's constant|2*[Bh]|1.0|
| [Pt] |Constant Value|Porter's constant|[Pt]*3|1.0|
| [L2] |Constant Value|Lieb's square ice constant|2*[L2]|1.0|
| [Nv] |Constant Value|Niven's constant|[Nv]*3|1.0|
| [Ks] |Constant Value|Sierpinski's constant|2*[Ks]|1.0|
| [Kh] |Constant Value|Khinchin's constant|[Kh]*3|1.0|
| [FR] |Constant Value|Fransen-Robinson constant|2*[FR]|1.0|
| [La] |Constant Value|Landau's constant|[La]*3|1.0|
| [P2] |Constant Value|Parabolic constant|2*[P2]|1.0|
| [Om] |Constant Value|Omega constant|[Om]*3|1.0|
| [MRB] |Constant Value|MRB constant|2*[MRB]|1.0|
| [li2] |Constant Value|li(2) - logarithmic integral function at x=2|[li2]*3|2.3|
| [EG] |Constant Value|Gompertz constant|2*[EG]|2.3|
| [true] | Constant Value | Boolean True represented as double, [true] = 1 | [true] | 4.1 |
| [false] | Constant Value | Boolean False represented as double, [false] = 0 | [false] | 4.1 |
| [NaN] | Constant Value | Not-a-Number | [NaN] | 4.1 |
## Physical Constant
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [c] |Constant Value|\ Light speed in vacuum [m/s] (m=1, s=1)|[c]*3|4.0|
| [G.] |Constant Value|\ Gravitational constant (m=1, kg=1, s=1)]|2*[G.]|4.0|
| [g] |Constant Value|\ Gravitational acceleration on Earth [m/s^2] (m=1, s=1)|[g]*3|4.0|
| [hP] |Constant Value|\ Planck constant (m=1, kg=1, s=1)|2*[hP]|4.0|
| [h-] |Constant Value|\ Reduced Planck constant / Dirac constant (m=1, kg=1, s=1)]|[h-]*3|4.0|
| [lP] |Constant Value|\ Planck length [m] (m=1)|2*[lP]|4.0|
| [mP] |Constant Value|\ Planck mass [kg] (kg=1)|[mP]*3|4.0|
| [tP] |Constant Value|\ Planck time [s] (s=1)|2*[tP]|4.0|
## Astronomical Constant
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [ly] |Constant Value|\ Light year [m] (m=1)|[ly]*3|4.0|
| [au] |Constant Value|\ Astronomical unit [m] (m=1)|2*[au]|4.0|
| [pc] |Constant Value|\ Parsec [m] (m=1)|[pc]*3|4.0|
| [kpc] |Constant Value|\ Kiloparsec [m] (m=1)|2*[kpc]|4.0|
| [Earth-R-eq] |Constant Value|\ Earth equatorial radius [m] (m=1)|[Earth-R-eq]*3|4.0|
| [Earth-R-po] |Constant Value|\ Earth polar radius [m] (m=1)|2*[Earth-R-po]|4.0|
| [Earth-R] |Constant Value|\ Earth mean radius (m=1)|[Earth-R]*3|4.0|
| [Earth-M] |Constant Value|\ Earth mass [kg] (kg=1)|2*[Earth-M]|4.0|
| [Earth-D] |Constant Value|\ Earth-Sun distance - semi major axis [m] (m=1)|[Earth-D]*3|4.0|
| [Moon-R] |Constant Value|\ Moon mean radius [m] (m=1)|2*[Moon-R]|4.0|
| [Moon-M] |Constant Value|\ Moon mass [kg] (kg=1)|[Moon-M]*3|4.0|
| [Moon-D] |Constant Value|\ Moon-Earth distance - semi major axis [m] (m=1)|2*[Moon-D]|4.0|
| [Solar-R] |Constant Value|\ Solar mean radius [m] (m=1)|[Solar-R]*3|4.0|
| [Solar-M] |Constant Value|\ Solar mass [kg] (kg=1)|2*[Solar-M]|4.0|
| [Mercury-R] |Constant Value|\ Mercury mean radius [m] (m=1)|[Mercury-R]*3|4.0|
| [Mercury-M] |Constant Value|\ Mercury mass [kg] (kg=1)|2*[Mercury-M]|4.0|
| [Mercury-D] |Constant Value|\ Mercury-Sun distance - semi major axis [m] (m=1)|[Mercury-D]*3|4.0|
| [Venus-R] |Constant Value|\ Venus mean radius [m] (m=1)|2*[Venus-R]|4.0|
| [Venus-M] |Constant Value|\ Venus mass [kg] (kg=1)|[Venus-M]*3|4.0|
| [Venus-D] |Constant Value|\ Venus-Sun distance - semi major axis [m] (m=1)|2*[Venus-D]|4.0|
| [Mars-R] |Constant Value|\ Mars mean radius [m] (m=1)|[Mars-R]*3|4.0|
| [Mars-M] |Constant Value|\ Mars mass [kg] (kg=1)|2*[Mars-M]|4.0|
| [Mars-D] |Constant Value|\ Mars-Sun distance - semi major axis [m] (m=1)|[Mars-D]*3|4.0|
| [Jupiter-R] |Constant Value|\ Jupiter mean radius [m] (m=1)|2*[Jupiter-R]|4.0|
| [Jupiter-M] |Constant Value|\ Jupiter mass [kg] (kg=1)|[Jupiter-M]*3|4.0|
| [Jupiter-D] |Constant Value|\ Jupiter-Sun distance - semi major axis [m] (m=1)|2*[Jupiter-D]|4.0|
| [Saturn-R] |Constant Value|\ Saturn mean radius [m] (m=1)|[Saturn-R]*3|4.0|
| [Saturn-M] |Constant Value|\ Saturn mass [kg] (kg=1)|2*[Saturn-M]|4.0|
| [Saturn-D] |Constant Value|\ Saturn-Sun distance - semi major axis [m] (m=1)|[Saturn-D]*3|4.0|
| [Uranus-R] |Constant Value|\ Uranus mean radius [m] (m=1)|2*[Uranus-R]|4.0|
| [Uranus-M] |Constant Value|\ Uranus mass [kg] (kg=1)|[Uranus-M]*3|4.0|
| [Uranus-D] |Constant Value|\ Uranus-Sun distance - semi major axis [m] (m=1)|2*[Uranus-D]|4.0|
| [Neptune-R] |Constant Value|\ Neptune mean radius [m] (m=1)|[Neptune-R]*3|4.0|
| [Neptune-M] |Constant Value|\ Neptune mass [kg] (kg=1)|2*[Neptune-M]|4.0|
| [Neptune-D] |Constant Value|\ Neptune-Sun distance - semi major axis [m] (m=1)|[Neptune-D]*3|4.0|
## Metric prefixes
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [%] |Unit|\ Percentage = 0.01|2*[%]|4.0|
| [%%] |Unit|\ Promil, Per mille = 0.001|[%%]*3|4.0|
| [Y] |Unit|\ Septillion / Yotta = 10^24|2*[Y]|4.0|
| [sept] |Unit|\ Septillion / Yotta = 10^24|[sept]*3|4.0|
| [Z] |Unit|\ Sextillion / Zetta = 10^21|2*[Z]|4.0|
| [sext] |Unit|\ Sextillion / Zetta = 10^21|[sext]*3|4.0|
| [E] |Unit|\ Quintillion / Exa = 10^18|2*[E]|4.0|
| [quint] |Unit|\ Quintillion / Exa = 10^18|[quint]*3|4.0|
| [P] |Unit|\ Quadrillion / Peta = 10^15|2*[P]|4.0|
| [quad] |Unit|\ Quadrillion / Peta = 10^15|[quad]*3|4.0|
| [T] |Unit|\ Trillion / Tera = 10^12|2*[T]|4.0|
| [tril] |Unit|\ Trillion / Tera = 10^12|[tril]*3|4.0|
| [G] |Unit|\ Billion / Giga = 10^9|2*[G]|4.0|
| [bil] |Unit|\ Billion / Giga = 10^9|[bil]*3|4.0|
| [M] |Unit|\ Million / Mega = 10^6|2*[M]|4.0|
| [mil] |Unit|\ Million / Mega = 10^6|[mil]*3|4.0|
| [k] |Unit|\ Thousand / Kilo = 10^3|2*[k]|4.0|
| [th] |Unit|\ Thousand / Kilo = 10^3|[th]*3|4.0|
| [hecto] |Unit|\ Hundred / Hecto = 10^2|2*[hecto]|4.0|
| [hund] |Unit|\ Hundred / Hecto = 10^2|[hund]*3|4.0|
| [deca] |Unit|\ Ten / Deca = 10|2*[deca]|4.0|
| [ten] |Unit|\ Ten / Deca = 10|[ten]*3|4.0|
| [deci] |Unit|\ Tenth / Deci = 0.1|2*[deci]|4.0|
| [centi] |Unit|\ Hundredth / Centi = 0.01|[centi]*3|4.0|
| [milli] |Unit|\ Thousandth / Milli = 0.001|2*[milli]|4.0|
| [mic] |Unit|\ Millionth / Micro = 10^-6|[mic]*3|4.0|
| [n] |Unit|\ Billionth / Nano = 10^-9|2*[n]|4.0|
| [p] |Unit|\ Trillionth / Pico = 10^-12|[p]*3|4.0|
| [f] |Unit|\ Quadrillionth / Femto = 10^-15|2*[f]|4.0|
| [a] |Unit|\ Quintillionth / Atoo = 10^-18|[a]*3|4.0|
| [z] |Unit|\ Sextillionth / Zepto = 10^-21|2*[z]|4.0|
| [y] |Unit|\ Septillionth / Yocto = 10^-24|[y]*3|4.0|
## Units of length
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m] |Unit|\ Metre / Meter (m=1)|2*[m]|4.0|
| [km] |Unit|\ Kilometre / Kilometer (m=1)|[km]*3|4.0|
| [cm] |Unit|\ Centimetre / Centimeter (m=1)|2*[cm]|4.0|
| [mm] |Unit|\ Millimetre / Millimeter (m=1)|[mm]*3|4.0|
| [inch] |Unit|\ Inch (m=1)|2*[inch]|4.0|
| [yd] |Unit|\ Yard (m=1)|[yd]*3|4.0|
| [ft] |Unit|\ Feet (m=1)|2*[ft]|4.0|
| [mile] |Unit|\ Mile (m=1)|[mile]*3|4.0|
| [nmi] |Unit|\ Nautical mile (m=1)|2*[nmi]|4.0|
## Units of area
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m2] |Unit|\ Square metre / Square meter (m=1)|[m2]*3|4.0|
| [cm2] |Unit|\ Square centimetre / Square centimeter (m=1)|2*[cm2]|4.0|
| [mm2] |Unit|\ Square millimetre / Square millimeter (m=1)|[mm2]*3|4.0|
| [are] |Unit|\ Are (m=1)|2*[are]|4.0|
| [ha] |Unit|\ Hectare (m=1)|[ha]*3|4.0|
| [acre] |Unit|\ Acre (m=1)|2*[acre]|4.0|
| [km2] |Unit|\ Square kilometre / Square kilometer (m=1)|[km2]*3|4.0|
## Units of volume
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [mm3] |Unit|\ Cubic millimetre / Cubic millimeter (m=1)|2*[mm3]|4.0|
| [cm3] |Unit|\ Cubic centimetre / Cubic centimeter (m=1)|[cm3]*3|4.0|
| [m3] |Unit|\ Cubic metre / Cubic meter (m=1)|2*[m3]|4.0|
| [km3] |Unit|\ Cubic kilometre / Cubic kilometer (m=1)|[km3]*3|4.0|
| [ml] |Unit|\ Millilitre / Milliliter (m=1)|2*[ml]|4.0|
| [l] |Unit|\ Litre / Liter (m=1)|[l]*3|4.0|
| [gall] |Unit|\ Gallon (m=1)|2*[gall]|4.0|
| [pint] |Unit|\ Pint (m=1)|[pint]*3|4.0|
## Units of time
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [s] |Unit|\ Second (s=1)|2*[s]|4.0|
| [ms] |Unit|\ Millisecond (s=1)|[ms]*3|4.0|
| [min] |Unit|\ Minute (s=1)|2*[min]|4.0|
| [h] |Unit|\ Hour (s=1)|[h]*3|4.0|
| [day] |Unit|\ Day (s=1)|2*[day]|4.0|
| [week] |Unit|\ Week (s=1)|[week]*3|4.0|
| [yearj] |Unit|\ Julian year = 365.25 days (s=1)|2*[yearj]|4.0|
## Units of mass
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [kg] |Unit|\ Kilogram (kg=1)|[kg]*3|4.0|
| [gr] |Unit|\ Gram (kg=1)|2*[gr]|4.0|
| [mg] |Unit|\ Milligram (kg=1)|[mg]*3|4.0|
| [dag] |Unit|\ Decagram (kg=1)|2*[dag]|4.0|
| [t] |Unit|\ Tonne (kg=1)|[t]*3|4.0|
| [oz] |Unit|\ Ounce (kg=1)|2*[oz]|4.0|
| [lb] |Unit|\ Pound (kg=1)|[lb]*3|4.0|
## Units of information
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [b] |Unit|\ Bit (bit=1)|2*[b]|4.0|
| [kb] |Unit|\ Kilobit (bit=1)|[kb]*3|4.0|
| [Mb] |Unit|\ Megabit (bit=1)|2*[Mb]|4.0|
| [Gb] |Unit|\ Gigabit (bit=1)|[Gb]*3|4.0|
| [Tb] |Unit|\ Terabit (bit=1)|2*[Tb]|4.0|
| [Pb] |Unit|\ Petabit (bit=1)|[Pb]*3|4.0|
| [Eb] |Unit|\ Exabit (bit=1)|2*[Eb]|4.0|
| [Zb] |Unit|\ Zettabit (bit=1)|[Zb]*3|4.0|
| [Yb] |Unit|\ Yottabit (bit=1)|2*[Yb]|4.0|
| [B] |Unit|\ Byte (bit=1)|[B]*3|4.0|
| [kB] |Unit|\ Kilobyte (bit=1)|2*[kB]|4.0|
| [MB] |Unit|\ Megabyte (bit=1)|[MB]*3|4.0|
| [GB] |Unit|\ Gigabyte (bit=1)|2*[GB]|4.0|
| [TB] |Unit|\ Terabyte (bit=1)|[TB]*3|4.0|
| [PB] |Unit|\ Petabyte (bit=1)|2*[PB]|4.0|
| [EB] |Unit|\ Exabyte (bit=1)|[EB]*3|4.0|
| [ZB] |Unit|\ Zettabyte (bit=1)|2*[ZB]|4.0|
| [YB] |Unit|\ Yottabyte (bit=1)|[YB]*3|4.0|
## Units of energy
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [J] |Unit|\ Joule (m=1, kg=1, s=1)|2*[J]|4.0|
| [eV] |Unit|\ Electronovolt (m=1, kg=1, s=1)|[eV]*3|4.0|
| [keV] |Unit|\ Kiloelectronovolt (m=1, kg=1, s=1)|2*[keV]|4.0|
| [MeV] |Unit|\ Megaelectronovolt (m=1, kg=1, s=1)|[MeV]*3|4.0|
| [GeV] |Unit|\ Gigaelectronovolt (m=1, kg=1, s=1)|2*[GeV]|4.0|
| [TeV] |Unit|\ Teraelectronovolt (m=1, kg=1, s=1)|[TeV]*3|4.0|
## Units of speed
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m/s] |Unit|\ Metre / Meter per second (m=1, s=1)|2*[m/s]|4.0|
| [km/h] |Unit|\ Kilometre / Kilometer per hour (m=1, s=1)|[km/h]*3|4.0|
| [mi/h] |Unit|\ Mile per hour (m=1, s=1)|2*[mi/h]|4.0|
| [knot] |Unit|\ Knot (m=1, s=1)|[knot]*3|4.0|
## Units of acceleration
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [m/s2] |Unit|\ Metre / Meter per square second (m=1, s=1)|2*[m/s2]|4.0|
| [km/h2] |Unit|\ Kilometre / Kilometer per square hour (m=1, s=1)|[km/h2]*3|4.0|
| [mi/h2] |Unit|\ Mile per square hour (m=1, s=1)|2*[mi/h2]|4.0|
## Units of angle
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| [rad] |Unit|\ Radian (rad=1)|[rad]*pi|4.0|
| [deg] |Unit|\ Degree of arc (rad=1)|180*[deg]|4.0|
| ['] |Unit|\ Minute of arc (rad=1)|[']*3|4.0|
| [''] |Unit|\ Second of arc (rad=1)|2*['']|4.0|
## Other parser symbols
|Key word|Category|Description|Example|Since|
|---|---|---|---|---|
| ( |Parser Symbol|Left parentheses|(3+2)/4|1.0|
| ) |Parser Symbol|Right parentheses|(3+2)/4|1.0|
| , |Parser Symbol|Comma (function parameters)|min(2,3,1)|1.0|
| ; |Parser Symbol|Semicolon (function parameters)|min(2;3;1)|1.0|
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# Enjoy :-)
Best regards,
*Mariusz Gromada* ](https://play.google.com/store/apps/details?id=org.mathparser.scalar.lite&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
### Scalar Pro - Full paid version
[
](https://play.google.com/store/apps/details?id=org.mathparser.scalar.lite&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
### Scalar Pro - Full paid version
[ ](https://play.google.com/store/apps/details?id=org.mathparser.scalar.pro&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
# MathParser.org-mXparser


# mXparser - optional donation
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser - a super easy, rich and highly flexible Mathematical Expression Parser (Math Parser, Expression Evaluator) library for JAVA, Android and C# .NET.
### 15.10.2020: first 500000 downloads!
### 20.12.2019: first 250000 downloads!
### 01.01.2019: first 100000 downloads!
### 01.08.2018: first 60000 downloads!
### 20.11.2017: first 20000 downloads!
### 01.09.2017: first 15000 downloads!
### 04.05.2017: first 10000 downloads!
### 31.03.2016: first 1000 downloads!

**mXparser** is **a highly flexible parser of mathematical expressions provided as text**. Software delivers easy to use API for JAVA and C# .NET.
# Supported frameworks

- JAVA: 6+
- Android - tested with mxparser compiled using jdk 1.7
- .NET Framework (2+) / MONO CLS
- .NET Core: 1+
- .NET Standard: 1+
- .NET PCL
- Xamarin

# JAVA intro

# C# intro

# Tutorial

# [>>> Click to learn from examples <<<](http://mathparser.org/mxparser-tutorial/)
# Main functionalities:
- **basic operators**, i.e.: +, -, *, ^, !
- **[Boolean logic](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BooleanAlgebra.html)** operators i.e.: or, and, xor
- **[binary relations](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BinaryRelations.html)** i.e.: =, <, >
- **[math functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html)** (large library of 1-arg, 2-arg, 3-arg - functions) i.e.: sin, cos, Stirling numbers, log, inverse functions
- **[constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathConstants.html)** (large library), i.e.: pi, e, golden ratio
- **n-args functions**, i.e.: [greatest common divisor](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html#gcd-int...-)
- **[iterated summation and product operators](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumberTheory.html#sigmaSummation-org.mariuszgromada.math.mxparser.Expression-org.mariuszgromada.math.mxparser.Argument-double-double-double-)**
- **[differentiation and integration](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumericalAnalysis.html)**
# High flexibility functionalities
- **[user defined constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Constant.html)** and arguments, both free - and dependent on other arguments + possibility of use in functions
- **[user defined functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html)** (both free and depended)
- **[user defined recursive arguments](http://mathparser.org/api/org/mariuszgromada/math/mxparser/RecursiveArgument.html)** + simple (controlled) recursion (1 recursive argument)
- **[user defined recursive functions / expressions (any)](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html#getRecursiveMode--)** - complex, many arguments, no limitation
- **[internal syntax checking](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#checkSyntax--)**
- **[internal help](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getHelp--)**
- other useful functionalities, i.e.: [computing time](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getComputingTime--), expression description.
# Project documentation
### - [mXparser - API (english)](http://mathparser.org/api/)
### - [mXparser - WIKI (english)](https://github.com/mariuszgromada/MathParser.org-mXparser/wiki)
### - [mXparser - Tutorial (english)](http://mathparser.org/mxparser-tutorial/)
### - [MathSpace.pl - site about math with mXparser examples (polish)](http://mathspace.pl/)
### - [MathParser.org - site about mXparser (english)](http://mathparser.org/)
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser in nutshell
#### You want simple calculator...
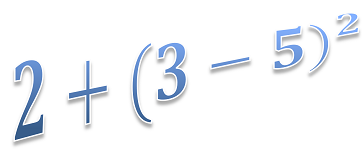
Expression e = new Expression("2+3");
e.calculate();
:+1:
#### A calculator supporting parenthesis...

Expression e = new Expression("2+(3-5)^2");
e.calculate();
:+1:
#### You care about predefined constants...

Expression e = new Expression("2*pi");
e.calculate();
:+1:
#### You need to define your own constants...
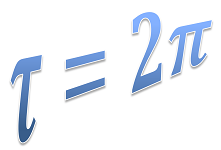
Constant tau = new Constant("tau = 2*pi");
Expression e = new Expression("3*tau", tau);
e.calculate();
:+1:
#### You enjoy using many built-in functions...

Expression e = new Expression("sin(2*pi)");
e.calculate();
:+1:
#### You do not limit yourself to unary functions...
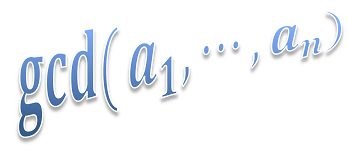
Expression e = new Expression("gcd(2,5,10,30)");
e.calculate();
:+1:
#### What about user defined arguments...
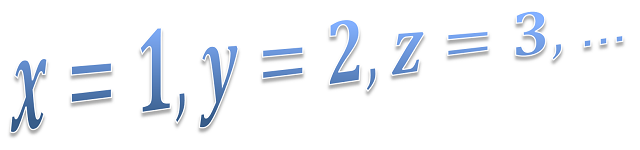
Argument x = new Argument("x = 5");
Expression e = new Expression("sin(x)");
e.calculate();
:+1:
#### You are considering dependent arguments...

Argument x = new Argument("x = 5");
Argument y = new Argument("y = 2*x", x);
Expression e = new Expression("sin(y)", y);
e.calculate();
:+1:
#### You need to apply some logic...

Argument x = new Argument("x = 5");
Expression e = new Expression("if(sin(x) > 5, 1, 0)", x);
e.calculate();
:+1:
#### Yes, you are right, there is a support for Boolean algebra!

Expression e = new Expression("5=6");
e.calculate();
:+1:
#### And for binary relations as well!
Expression e = new Expression("5 <= 6");
e.calculate();
:+1:
## mXparser is cool! But this is only the begging, we are just warming up!
#### You want to play with iterated operators...

Expression e = new Expression("sum(i, 1, 10, 2*i^2 + pi)");
e.calculate();
:+1:
#### You want to iterate differently by not necessarily whole numbes...

Expression e = new Expression("prod(i, 1, 5, i, 0.5)");
e.calculate();
:+1:
#### You want to have more fun with math...
Argument x = new Argument("x = pi/2");
Expression e20 = new Expression("sum(n,0,10,(-1)^n*(x^(2*n+1))/(2*n+1)!)", x);
e.calculate();
:+1:
#### You still want more fun with calculus operations, i.e. differentiation...
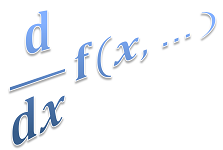
Argument x = new Argument("x = pi/2");
Expression e = new Expression("cos(x)-der(sin(x), x)", x);
e.calculate();
:+1:
#### And definite integrals as well...
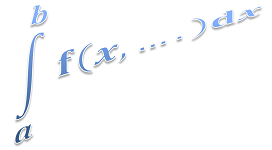
Expression e = new Expression("2*int(sqrt(1-x^2), x, -1, 1)");
e.calculate();
:+1:
## mXparser is even cooler! It is time to ask about ...
#### user defined functions...
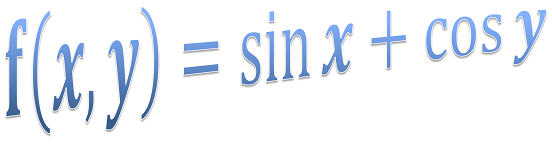
Function f = new Function("f(x,y) = sin(x) + cos(y)");
f.calculate(1,2);
Expression e = new Expression("f(1,2) - 10", f);
e.calculate();
:+1:
#### Recursion is your desire...
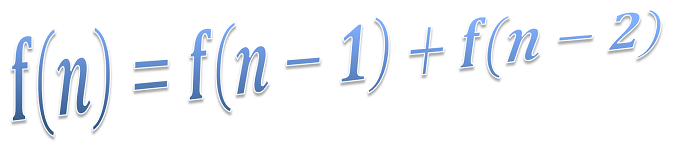
Function f = new Function("f(n) = if( n>0, n*f(n-1), 1)");
f.calculate()
:+1:
#### Any kind of recursion...
Function Cnk = new Function("Cnk(n,k) = if(k>0, if(k
](https://play.google.com/store/apps/details?id=org.mathparser.scalar.pro&pcampaignid=MKT-Other-global-all-co-prtnr-py-PartBadge-Mar2515-1)
# MathParser.org-mXparser


# mXparser - optional donation
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser - a super easy, rich and highly flexible Mathematical Expression Parser (Math Parser, Expression Evaluator) library for JAVA, Android and C# .NET.
### 15.10.2020: first 500000 downloads!
### 20.12.2019: first 250000 downloads!
### 01.01.2019: first 100000 downloads!
### 01.08.2018: first 60000 downloads!
### 20.11.2017: first 20000 downloads!
### 01.09.2017: first 15000 downloads!
### 04.05.2017: first 10000 downloads!
### 31.03.2016: first 1000 downloads!

**mXparser** is **a highly flexible parser of mathematical expressions provided as text**. Software delivers easy to use API for JAVA and C# .NET.
# Supported frameworks

- JAVA: 6+
- Android - tested with mxparser compiled using jdk 1.7
- .NET Framework (2+) / MONO CLS
- .NET Core: 1+
- .NET Standard: 1+
- .NET PCL
- Xamarin

# JAVA intro

# C# intro

# Tutorial

# [>>> Click to learn from examples <<<](http://mathparser.org/mxparser-tutorial/)
# Main functionalities:
- **basic operators**, i.e.: +, -, *, ^, !
- **[Boolean logic](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BooleanAlgebra.html)** operators i.e.: or, and, xor
- **[binary relations](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/BinaryRelations.html)** i.e.: =, <, >
- **[math functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html)** (large library of 1-arg, 2-arg, 3-arg - functions) i.e.: sin, cos, Stirling numbers, log, inverse functions
- **[constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathConstants.html)** (large library), i.e.: pi, e, golden ratio
- **n-args functions**, i.e.: [greatest common divisor](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/MathFunctions.html#gcd-int...-)
- **[iterated summation and product operators](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumberTheory.html#sigmaSummation-org.mariuszgromada.math.mxparser.Expression-org.mariuszgromada.math.mxparser.Argument-double-double-double-)**
- **[differentiation and integration](http://mathparser.org/api/org/mariuszgromada/math/mxparser/mathcollection/NumericalAnalysis.html)**
# High flexibility functionalities
- **[user defined constants](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Constant.html)** and arguments, both free - and dependent on other arguments + possibility of use in functions
- **[user defined functions](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html)** (both free and depended)
- **[user defined recursive arguments](http://mathparser.org/api/org/mariuszgromada/math/mxparser/RecursiveArgument.html)** + simple (controlled) recursion (1 recursive argument)
- **[user defined recursive functions / expressions (any)](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Function.html#getRecursiveMode--)** - complex, many arguments, no limitation
- **[internal syntax checking](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#checkSyntax--)**
- **[internal help](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getHelp--)**
- other useful functionalities, i.e.: [computing time](http://mathparser.org/api/org/mariuszgromada/math/mxparser/Expression.html#getComputingTime--), expression description.
# Project documentation
### - [mXparser - API (english)](http://mathparser.org/api/)
### - [mXparser - WIKI (english)](https://github.com/mariuszgromada/MathParser.org-mXparser/wiki)
### - [mXparser - Tutorial (english)](http://mathparser.org/mxparser-tutorial/)
### - [MathSpace.pl - site about math with mXparser examples (polish)](http://mathspace.pl/)
### - [MathParser.org - site about mXparser (english)](http://mathparser.org/)
[](https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted_button_id=QJYYH86583LEN)
# mXparser in nutshell
#### You want simple calculator...
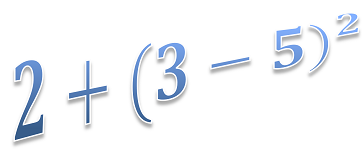
Expression e = new Expression("2+3");
e.calculate();
:+1:
#### A calculator supporting parenthesis...

Expression e = new Expression("2+(3-5)^2");
e.calculate();
:+1:
#### You care about predefined constants...

Expression e = new Expression("2*pi");
e.calculate();
:+1:
#### You need to define your own constants...
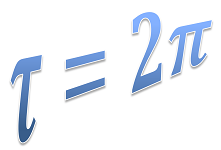
Constant tau = new Constant("tau = 2*pi");
Expression e = new Expression("3*tau", tau);
e.calculate();
:+1:
#### You enjoy using many built-in functions...

Expression e = new Expression("sin(2*pi)");
e.calculate();
:+1:
#### You do not limit yourself to unary functions...
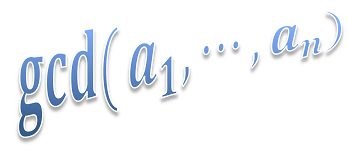
Expression e = new Expression("gcd(2,5,10,30)");
e.calculate();
:+1:
#### What about user defined arguments...
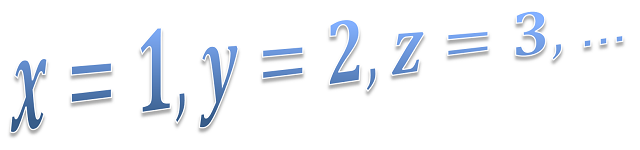
Argument x = new Argument("x = 5");
Expression e = new Expression("sin(x)");
e.calculate();
:+1:
#### You are considering dependent arguments...

Argument x = new Argument("x = 5");
Argument y = new Argument("y = 2*x", x);
Expression e = new Expression("sin(y)", y);
e.calculate();
:+1:
#### You need to apply some logic...

Argument x = new Argument("x = 5");
Expression e = new Expression("if(sin(x) > 5, 1, 0)", x);
e.calculate();
:+1:
#### Yes, you are right, there is a support for Boolean algebra!

Expression e = new Expression("5=6");
e.calculate();
:+1:
#### And for binary relations as well!
Expression e = new Expression("5 <= 6");
e.calculate();
:+1:
## mXparser is cool! But this is only the begging, we are just warming up!
#### You want to play with iterated operators...

Expression e = new Expression("sum(i, 1, 10, 2*i^2 + pi)");
e.calculate();
:+1:
#### You want to iterate differently by not necessarily whole numbes...

Expression e = new Expression("prod(i, 1, 5, i, 0.5)");
e.calculate();
:+1:
#### You want to have more fun with math...
Argument x = new Argument("x = pi/2");
Expression e20 = new Expression("sum(n,0,10,(-1)^n*(x^(2*n+1))/(2*n+1)!)", x);
e.calculate();
:+1:
#### You still want more fun with calculus operations, i.e. differentiation...
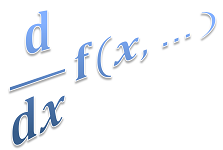
Argument x = new Argument("x = pi/2");
Expression e = new Expression("cos(x)-der(sin(x), x)", x);
e.calculate();
:+1:
#### And definite integrals as well...
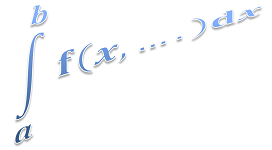
Expression e = new Expression("2*int(sqrt(1-x^2), x, -1, 1)");
e.calculate();
:+1:
## mXparser is even cooler! It is time to ask about ...
#### user defined functions...
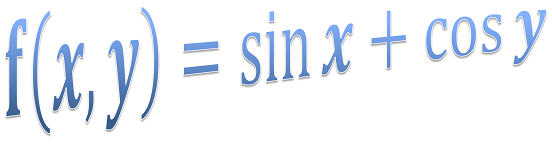
Function f = new Function("f(x,y) = sin(x) + cos(y)");
f.calculate(1,2);
Expression e = new Expression("f(1,2) - 10", f);
e.calculate();
:+1:
#### Recursion is your desire...
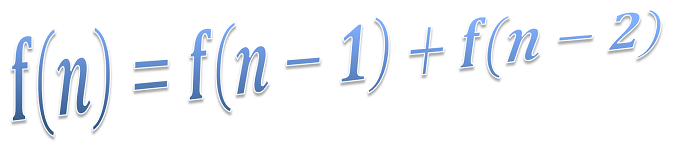
Function f = new Function("f(n) = if( n>0, n*f(n-1), 1)");
f.calculate()
:+1:
#### Any kind of recursion...
Function Cnk = new Function("Cnk(n,k) = if(k>0, if(k